proszę o szczegółowe wyjaśnienie study 1350: dany jest trójkąt prostokątny równoramienny ABC, którego przeciwprostokątna AB ma długość pierwiastek z 2 =. Dwusieczna kąta ABC przecina bok AC w punkcie P. Oblicz obwody trójkątów BCP i BAP.

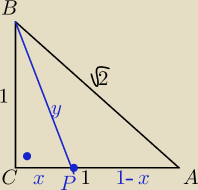
a7: korzystamy z tw. o dwusiecznej https://matematykaszkolna.pl/strona/498.html x/1=(1−x)/√2 xp{2]+x=1

	1		1		√2−1
x=		=		*		=√2−1
	(√2+1)		(√2+1)		√2−1

z tw. Pitagorasa dla ΔBCP y²=1²+x² y²=1+(√2−1)² y²=4−2√2 y=√4−2√2 OBW_BPC=1+√2−1+√4−2√2=√2+√2(2−√2)=√2(1+√2−√2) OBW_BPA=√2+1−(√2−1)+√4−2√2=√2+ 1−√2+1+√2(2−√2=2+√2(2−√2)

study: niezbyt rozumiem to wyjaśnienie

a7: 1. BC=CA=1 czy to rozumiesz? czy to się zgadza (trójkąt jest równoramienny, a przeciwprostokątna √2 z tw. Pitagorasa a² +a²=(√2)² czyli a=1 2. korzystamy z tw. o dwusiecznej

x		1−x
	=		wyliczamy x i wychodzi x=√2−1
1		√2

3.Z tw. Piagorasa obliczamy y y=√2(2−√2 4.Obliczamy Obwody co jest niejasne? który punkt?

study: tak to rozumiem dziękuję

a7: ok, fajnie