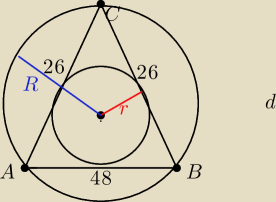
Okrąg wpisany i opisany - trójkąt ihaveapen: W trójkącie ABC mamy dane jak na rysunku. Chcę obliczyć promień okręgu wpisanego w trójkąt i

	1
opisanego na nim. Obliczyłem, że r wynosi 23		, a R wynosi ≈7,04. Czy jest to poprawny
	25

wynik? Podstawiłem pod wzory i tyle mi wyszło, ale jakbyście mogli rzucić okiem i potwierdzić, bo mam wątpliwości :0

ihaveapen: d narysowałem z boku niechcący − nie zwracajcie uwagi

ihaveapen: Nie wiem, mogłem coś pomylić, bo to nie wygląda na dobre wyniki, nie pasuje

Bogdan:

	1
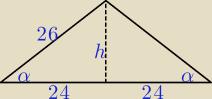
h2 = 262 − 242 = 100 ⇒ h = 10, p =		(26 + 26 + 48) = 50
	2

	26*26*24
Pole trójkąta 24*10 = r*p oraz 24*10 =
	4R

	10		26
Można także skorzystać z twierdzenia sinusów: sinα =		, 2R =
	26		sinα

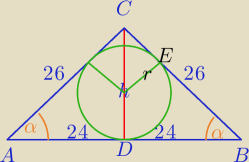Mila: 1) W ΔCDB: h²=26²−24²=100 h=10

	1
2) PΔABC=		*48*10=240
	2

	2*26+48
240=		*r ⇔240=50*r
	2

	24
r=
	5

===== 3) W ΔADC:

	10		5
sinα=		=
	26		13

W ΔABC:

|BC|		26
	=2R ⇔		=2R
sinα		5   13

	26*13
2R=
	5

	169
R=
	5

Albo z wzoru:

	a*b2
PΔ=
	4R

	48*262
240=
	4R

4R*240=48*13²*2² R*10=2*13²

	169
R=
	5

=======