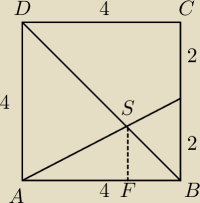
Pole kwadratu ABCD jest równe 16. Punkt E jest środkiem boku BC , a punkt S punktem
przecięcia przekątnej BD kwadratu i odcinka AE . Wykaż, że odległość punktu S od boku AB
| 4 | ||
jest równa | . | |
| 3 |
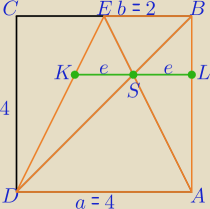Można skorzystać z własności trapezu: |KS| = |KL| i długość odcinka równoległego do
podstaw trapezu i przechodząca przez punkt S przecięcia przekątnych jest równa średniej
| 2ab | ab | |||
harmonicznej długości podstaw: |KL| = | ⇒ e = | |||
| a + b | a + b |
| 4*2 | 8 | 4 | ||||
W tym zadaniu e = | = | = | ||||
| 4 + 2 | 6 | 3 |
3
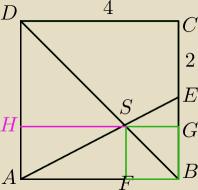
| 4 | ||
ΔADS jest podobny do ΔBSE w skali 2, SG jest więc równe 2*|SH| SG+SH=4 SG+2SG=4 SG= | ||
| 3 |
| 4 | ||
|SF|=|SG|= | (gdyż trójkąty SFB i SGB są przystające (k,b,k) | |
| 3 |
FBGS jest kwadratem.
