Proszę o pomoc Pomocy : W nieskończonym ciągu geometrycznym (an) a1=p + 2 i a2 = (p² + 2p):(p−1). Dla jakich wartości parametru p szereg a1+a2+a3+... Jest zbieżny?

Jerzy:

	a2
q =		i teraz warunek: |q| < 1
	a1

ICSP: dla p = −2 jest zbieżny. Dla p ≠ −2

	a2
q =		= p(p−1)
	a1

|q| < 1 ⇒ |p² − p| < 1 ⇒ (p² − p + 1)(p² − p −1) < 0 ⇒ p² − p − 1 < 0

	1		1
p ∊ (		(1 − √5) ;		(1 + √5)) ∪ {−2}
	2		2

Pomocy : A nie powinno wyjść q = p:(p−1)?

ICSP: tam jest dzielenie

	p
q =
	p − 1

to jeszcze p ≠ 1 dochodzi.

Pomocy : Dzielenie, może słabo było widać na początku. To pierwsze rozwiązanie jest błędne?

ICSP: rozwiązanie błędne ale sam schemat jak najbardziej poprawny.

Pomocy : W jaki sposób |p:(p−1)|<1 rozpisać?

Jerzy: |a| < 1 ⇔ − 1 < a < 1

Pomocy : Nie rozumiem za bardzo czy ktoś mógłby przybliżyć?

Pomocy : Czy mogę sobie zamienić p:(p−1) na 1−p?

Jerzy:

	p
− 1 <		< 1 i rozbij na dwie nierówności.
	p − 1

Pomocy : −1<p/(p−1) i p/(p−1)<1?

Pomocy : Tak będzie?

Jerzy: Tak będzie , a wynik końcowy, to część wspólna rozwiązań tych nierówności.

Pomocy : Chyba coś źle robię bo z jednej nierównosci p mi wychodzi <1 a w drugiej >1

Jerzy: Pokaż rachunki.

Jerzy: Obawiam się,że mnożysz obustronnie przez: p − 1 , a to jest niedopuszczalne !

Pomocy : A mógłbyś napisać swoje rachunki? Wystarczy że zerknę na swoje i znajdę błąd

Pomocy : Mnożę p−1 ale do kwadratu

Pomocy : I mogę tak zrobić

Jerzy: No to pokaż te rachunki.

Pomocy:

p
	+1 > 0 /* (p−1)2
p − 1

p*(p−1) + (p−1)² > 0 p² − p + p² − 2p +1 > 0 2p² − 3p + 1> 0 delta = 1 x1 = 1/2 x2 = 1

Pomocy: to pierwsze

Pomocy:

p
	< 0 /* (p−1)2
p − 1

p*(p − 1) − 1(p − 1)² < 0 p² − p −1(p² − 2p +1) < 0 p² − p − p² +2p − 1<0 p − 1 < 0 p < 1

Pomocy: a w pierwszym jest p>1/2 i p>1

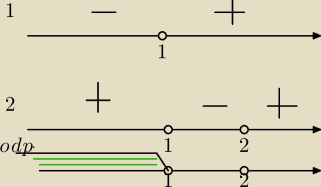
a7: moim zdaniem to powinno być tak:

	p(p+2)
|		|<1
	(p−1)(p−2)

	p(p+2)
−1<		<1
	(p−1)(p−2)

	p(p+2)
1.		<1
	(p−1)(p−2)

zał p≠1 i p≠2

(p2+2p−p2+3p−2)
	<0
(p−1)(p−2)

1
	<0
p−1

p∊(−∞,1)

	p(p+2)
2.		>−1 zał p≠1 i p≠2
	(p−1)(p−2)

(2p2−p+2)
	>0
(p−1)(p−2)

Δ_licznika<0 czyli licznik większy 0 p∊(−∞, 1) lub (2,∞) odp p∊(−∞,1)

Pomocy : A czemu (2,∞) się nie zalicza?

Pomocy : I czemu w mianowniku dałeś (p−1)(p−2) na samym początku?

Pomocy : Skoro a1 jest równe p+2

Pomocy : To chyba coś źle jest

ICSP: Chyba żartujecie.

	p
|		| < 1 dla p ≠ 1
	p−1

|p| < |p−1| // ² p² < p² − 2p + 1 2p < 1

	1
p <
	2

Pomocy : Można pomnożyć razy |p−1|?

ICSP: no a dlaczego nie?

Pomocy : Normalnie w nierównościach się tak nie robi ale może jak jest wartość bezwzględna to jest taka możliwość

Jerzy: Każdą nierówność możesz obustronnie pomnożyć przez liczbę różną od zera jeśli ma stały znak.

Jerzy: Ano właśnie dlatego, bo moduł różny od zera jest dodatni.

a7: u mnie oczywiście całe rozwiązanie złe przez ten minus zamiast plusa