badanie trójmianu kwadratu Malaa: Narysuj wykres funkcji f(x) = ( i tutaj taki duży "nawias" −> { x² − 2x dla x e (−oo, 3) −x+6 dla x e <3,+oo ) jak to narysować mam później polecenia do wykresu..ale u mnie jest problem z narysowaniem go o co chodzi jak są dwa przedziały jak to się robi proszę o wytłumaczenie

Malaa:

edi: Rysujesz dwa wykresy na jednym układzie współrzędnych: x² − 2x oraz −x + 6. Teraz weź jakiś kolor. Popatrz na wykres funkcji x² − 2x. Zaznacz kółkiem wartość wykresu tej funkcji dla argumentu 3. Cały wykres na lewo od kółka również zaznaczasz kolorem. Analogicznie z drugim wykresem, tylko, że malujesz wszystko na prawo od kółka, a samo kółko dla 3 ma być zamalowane.

Malaa: próbowałam to narysować..ale coś mi nie wychodzi.. chyba nie dokładnie rozumiem co masz na mysli.. mógłbyś mi narysować jeden wykres a ja już postaram sie narysowac wykresy w kolejnych zadaniach... bardzo Cię proszę

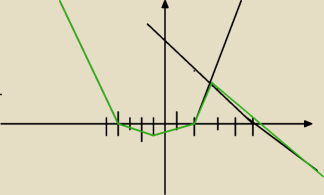
Malaa: czy to powinno mniej wiecej wygladac tak

Malaa: oczywiscie to nieudane coś..to parabola.. a obok juz wykres funkcji liniowej.. nie wiem czy dobrze zaznaczylam tym kolorem.....

edi: Nie wiem jak tutaj rysować wykresy, więc musiałem wykorzystać inny sposób: http://zapodaj.net/images/992c0fbc31ad.jpg : )

edi: tak, dokładnie tak powinno to wyglądać

edi: Zły link. Poprawna wersja: http://zapodaj.net/992c0fbc31ad.jpg.html

Malaa: dziękuję jesteś boski,że chciało Ci się to narysować i zeskanować ! ( sądząc po nicku boski−a nie boska.. jeśli jest inaczej to przepraszam za pomyłkę ) i jeszcze jedno.. skąd wiemy w którą stronę to ma iść.. że lewa .. prawa etc. ?

Malaa: i jak potem do takiej funkcji znaleźć miejsca zerowe bo z wykresu chyba nie da sie odczytać dokładnie... a wyliczanie delty etc. też mi tutaj zbytnio nie pasuje −.− do tego są jakby na to podane dwa wzory...

Malaa: chyba wiem obliczam z delty dwa miejsca zerowe do funkcji kwadratowej.. i jedno miejsce zerowe do liniowej, tak i wszystkie trzy są miejscami zerowymi ?

darek: na wykresie miejsca zerowe jest to 'przeciecie' prostej / paraboli z osia X, obliczeniowo oblicz delte x1 i x2 i masz

edi: Skąd wiadomo czy od lewej, czy od prawej − tak na prawdę rysujesz tylko fragment funkcji wskazany przez zakres − czyli jak kwadratowa ma być od −∞ do 3, to rysujesz jej wykres tylko dla x z przedziału od −∞ do 3. Jak wiadomo −∞ jest po lewej stronie osi ox, dlatego też wykres ten szedł od lewej strony Co do miejsc zerowych. Liczysz miejsca zerowe obu funkcji i jeżeli znajdują się one w zakresie danej funkcji, to będą miejscami zerowymi tej "zlepionej" funkcji. Spróbuj dla treningu narysować te same funkcje tylko w takich zakresach: x² − 2x dla x ∊ (−∞;1) −x + 6 dla x∊<1;∞) x² − 2x dla x∊(−∞;−2) −x + 6 dla x∊<−2;∞)

darek: jeli dobrze patrze to w tym wypadku miejscami zerowymi beda punkty (0;0), (0;2) i (0;6)

Nusiek: już rysuję ... i wrzucę link. więc poczekaj chwilkę ; ) bo dopiero teraz przeczytałam wiadomość

Malaa: http://zapodaj.net/8c9085e0d98d.jpg.html mniej więcej tak ? haha.. i źle przepisałam co napisałeś.. ale dla czegoś takiego by to wyglądało w ten sposób ?

edi: Ty zrobiłaś wersję dla y należącego do podanych zakresów, a ma być dla x Zakresy które napisałaś "nachodzą się" na siebie − to znaczy, że dla x ∊ <−2;1) znajdują się dwie funkcje, a tak nie może być Już prawie dobrze, teraz tylko przestaw y na x i będzie ok : >

Malaa: hmmmmmmmmmmmmmmmmmmm. bo później narysowałam to dla x2 − 2x dla x ∊ (−∞;1) −x + 6 dla x∊<1;∞) tylko że wyszło coś takiego : http://zapodaj.net/8921d13ece82.jpg.html a skoro tamto było źle..to to też będzie. tylko zę z tymi 3 to się tak ładnie przecinało..bo z obliczeń wychodziło ze tam musi się przeciąć.. a jak mam te jedynki to jest gorzej −.−

Malaa: i tam jest źle podpisane : jest dokładnie to : x2 − 2x dla x ∊ (−∞;1) −x + 6 dla x∊<1;∞) tylko patrzyłam sie na poprzedni rysunek i przepisałam to nieświadomie

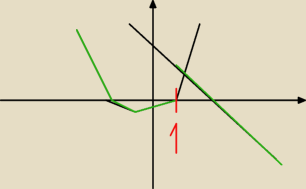
Malaa: rozumiem o co Ci chodzi teraz z tym x... tylko ze nie wiem jak to bedzie wygladalo....... tzn. ja patrzyłam na wartosci y − racja.. powinnam na x.. ale jakbym patrzyła na x to według mnie wyszloby coś takiego.. − dziwnego inaczej mówiąc.

edi: właśnie tak powinno wyjść Jest jeszcze kwestia, co dzieje się z funkcją w punkcie, w którym następuje zmiana: otóż tam gdzie przedział jest otwarty (w tym przypadku dla (−∞;1) ) na końcu rysujemy okrąg, a na początku funkcji z zamkniętym zakresem (w tym przypadku <1;∞) ) rysujemy zamalowane kółko

Malaa: hehe, dziękuję : * już chyba to rozumiem

edi: nie ma za co : )