stereometria kuba: Krawędź boczna ostrosłupa prawidłowego trójkątnego jest dwa razy dłuższa od krawędzi podstawy, której długość jest równa a. Oblicz pole przekroju tego ostrosłupa płaszczyzną, która przechodzi przez krawędź podstawy i jest prostopadła do krawędzi bocznej. (Odp a² * √11 / 8 )

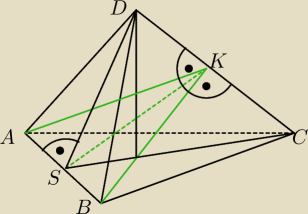
getin: |AB| = |BC| = |AC| = a |AD| = |BD| = |CD| = 2a |SK| = h |DS| = x |CK| = m |DK| = 2a−m

	a*√3
|SC| =
	2

|AS|² + |DS|² = |AD|²

	a
(		)2 + x2 = (2a)2
	2

	√15
x =		a
	2

|SK|² + |CK|² = |SC|²

	a*√3
h2 + m2 = (		)2
	2

	3
h2 + m2 =		a2
	4

|SK|² + |DK|² = |DS|² h² + (2a−m)² = x²

	√15
h2 + 4a2 − 4a*m + m2 = (		a)2
	2

	15
h2 + m2 + 4a2 − 4a*m =		a2
	4

3		15
	a2 + 4a2 − 4a*m =		a2
4		4

	1
m =		a
	4

	3
h2 + m2 =		a2
	4

	1		3
h2 + (		a)2 =		a2
	4		4

	11
h2 =		a2
	16

	√11
h =		a
	4

	1
PABK =		a*h
	2

	1		√11		a2 * √11
PABK =		a*		a =
	2		4		8

kuba: Dzięki bardzo!

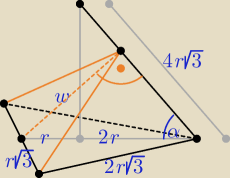Bogdan: Duzy wpływ na sposób rozwiązania mają przyjęte oznaczenia.

	1
r − długość promienia okręgu wpisanego w podstawę ostrosłupa, r =		a√3 ⇒ a = 2r√3
	6

	a2
r2 =		, α∊(0o, 90o),
	12

	2r		1		√11
cosα =		=		, sinα =
	4r√3		2√3		2√3

	√11		√3*√11
w = 3r*sinα = 3r*		= r*
	2√3		2

Pole przekroju

	√3*√11		3		3		a2
P = r√3*w = r√3*r*		=		r2√11 =		*		√11 =
	2		2		2		12

	a2√11
=
	8

Eta: dla Bogdana

Bogdan: