Równoleglobok
Agnieszka: Dany jest równoległobok ABCD o kącie ostrym w wierzchołku A równym 45 stopni
Wewnątrz równoległoboku znajduje się punkt P, którego odległości od boków AB i AD wynoszą
odpowiednio i 2. Oblicz długość odcinka AP.
27 maj 10:59
getin:
wynoszą odpowiednio i 2
Nie brakuje tu jakiejś liczby w poleceniu ?
27 maj 12:16
Agnieszka : Coś musiało się nie wpisać miało być √2
27 maj 13:01
getin:
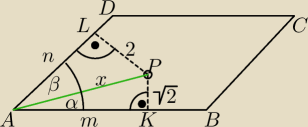
α + β = 45
o
β = 45
o − α
|AP| = x = ?
| | √2 | | m | | √2 | | √2 | |
sinβ = sin(45o−α) = sin45o*cosα − sinα*cos45o = |
| * |
| − |
| * |
| = |
| | 2 | | x | | x | | 2 | |
| | m*√2 | | 1 | | m*√2−2 | |
= |
| − |
| = |
| (wzór na sinus różnicy) |
| | 2x | | x | | 2x | |
zaś z ΔALP
zatem
m*
√2−2 = 4
m = 3
√2
W ΔAPK:
x
2 = m
2 + (
√2)
2
x = 2
√5
27 maj 13:15
Eta:
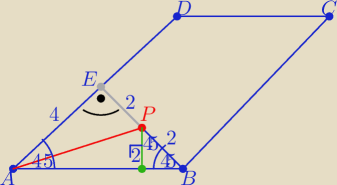
Prawie bez obliczeń

trójkąt ABE "ekierkowy" o katach ostrych 45
o,45
o
to oznaczenia na rysunku
zatem: |AP|=
√42+22=
√20
|AP|=2
√5
============
27 maj 13:40
 α + β = 45o
β = 45o − α
|AP| = x = ?
α + β = 45o
β = 45o − α
|AP| = x = ?
 Prawie bez obliczeń
Prawie bez obliczeń  trójkąt ABE "ekierkowy" o katach ostrych 45o,45o
to oznaczenia na rysunku
zatem: |AP|= √42+22=√20
|AP|=2√5
============
trójkąt ABE "ekierkowy" o katach ostrych 45o,45o
to oznaczenia na rysunku
zatem: |AP|= √42+22=√20
|AP|=2√5
============