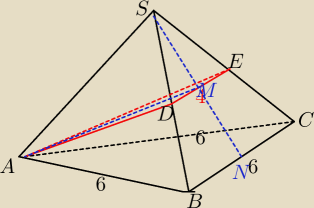
stereometria - znalezienie błędu m: Podstawą ostrosłupa prawidłowego ABCS jest trójkąt równoboczny ABC o boku długości 6. Na krawędziach bocznych BS i CS wybrano punkty, odpowiednio D i E , takie że |BD | = |CE | oraz |DE | = 4 (zobacz rysunek). Płaszczyzna ADE jest prostopadła do płaszczyzny ściany bocznej BCS ostrosłupa. Zrobiłam to zadanie, tylko nie widzę gdzie popełniłam błąd, proszę o wskazanie go. DE SM 2 −−− = −−− = −−− BC SN 3 SM = 2/3 h_b MN = 1/3 h_b AM² = l² − 4/9 h_b² AM² = 27 − 1/9 h_b² l² = 9+h_b² 9 + h_b² − 4/9h_b² = 27 − 1/9h_b² 2/3 h_b² =18 h_b² = 27 h_b = 3 √3 Według odpowiedzi h_b = 2√3

sntr37: Twoja odpowiedź jest prawidłowa. Ten ostrosłup jest czworościanem foremnym.

a7: |AS|²=|AM|²+|SM|² |BS|²=|AS|²=9+h_b² |AS|=|BS|=k AM=d d²=27−1/9h_b² k²=d²+4/9h_b k²=9+(h_b)² 27−1/9h_b²+4/9h_b²=9+(h_b)² h_b=2√3

sntr37: a7 popełniłeś błąd: Jeśli: d²=27−1/9h_b² k²=d²+4/9h_b k²=9+(h_b)² to: d²+4/9h_b=9+(h_b)² d²=9+5/9h_b² czyli: 9+5/9h_b² = 27−1/9h_b² 18=6/9h_b² |:6 3=1/9h_b² |*9 27=h_b² h_b=3√3

a7: tak, źle przeniosłam na drugą stronę 3/9(h_b)², także u mnie źle

janusz: Czy jeśli wysokość trójkąta BCS dzieli się w stosunku 2:1 to można uznać że jest to trójkąt równoboczny, a cały ostrosłup jest czworościanem foremnym?

janusz: Odpowie ktoś?