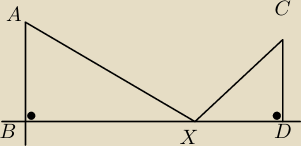
Punkty A, B, C, D położone są jak na rysunku obok. Zakładamy, że AB AB⊥BD, CD⊥BD oraz|AB|=5,
|CD|=3, |BD|=11. Niech punkt X należy do odcinka BD.
a)Wykaż, że suma |AX|+|XC| jest najmniejsza wtedy i tylko wtedy, gdy |∠ BXA|=| ∠ DXC|.
b)Oblicz długość odcinka BX, dla którego suma |AX|+|XC| jest najmniejsza.
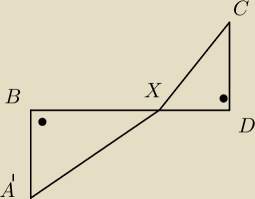A' jest symetryczny do A względem prostej BD