Prawdopodobieństwo- definicja. Wskaż, żę... Jokur: O zdarzeniach A,B⊂Ω wiemy, że P(A)=0,6 oraz P(A∩B)=0,2. Wskaż równość, która musi być fałszywa. A. P(A−B)=0,4 B. P(A∪B)=1 C. P(B−A)=0,1 D. P(B)=0,7 Umiem sobie rozpisać P(A−B) itd i dowiodłem, że A jest prawdziwe, ale nie wiem jak obliczyć P(B). Dostałem jakiegoś zaćmienia i nie wiem co z tym zrobić.

Qulka: max to 1=0,6+x−0,2 więc P(B) to max 0,6

Qulka: ostatni wzór https://matematykaszkolna.pl/strona/1018.html

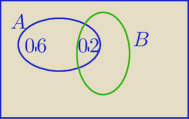
Mila: P(A∪B)=P(A)+P(B)− P(∩B) 1) P(A\B)=P(A)−P(∩B)=0.6−0.2=0.4 odp. A− P sprawdzam odp. D P(A∪B)=0.6+x −0.2 P(A∪B)=0.6+0.7−0.2=1,1 >1 D− fałsz =============== B i C 0.6+x −0.2≤1⇔x≤1−0.4=0.6 0.2≤P(B)≤0.6 dla P(B)=0.6 mamy P(A∪B)=0.6+0.6−0.2=1 może zachodzić I C też może zachodzić dla P(B)=0.3

Jokur: Dziękuję ślicznie