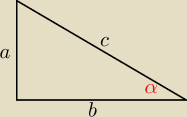
sinsuy fil: Wyznacz sinusy katów ostrych trójkata prostokatnego wiedzac, ze stosunek promieni okregów

	13
opisanego i wpisanego w ten trójkat jest równy
	4

Wie ktos gdzie jest blad?

R		13
	=
r		4

	13
2R = c =		r
	2

	a		2		a
sinα =		=		* (		)
	c		13		r

	a + b − c
r =
	2

2r + c = a + b

	17		17
a + b =		r => b =		r − a
	2		2

Pitagoras:

	17		169
a2 + (		r − a)2 =		r2
	2		4

2a² − 17ar + 30r² = 0 | /r²

	a2		a
2		− 17		+ 30 = 0
	r2		r

	a		13		13
Podstawienie t =		−−> t ∊ (−		,		)
	r		2		2

2t² − 17t + 30 = 0 Δ = 169

	17 − 13
t1 =		= 1
	4

	30
t2 =
	4

Nie zgadzaja mi sie wartosci sinusa

fil:

	2
sinα =
	13

fil:

	π
Chyba ze sinβ obliczyc z sin(		− α)
	2

ICSP: 17² − 30*8 = ?

fil: kurde, cos namieszalem ostro, no dobra w takim razie Δ = 49

	5
t1 =
	2

t₂ = 6

fil:

	5
sinα =		, jednak co z sinusem drugiego kata?
	13

ICSP:

	2		12
sinα =		* 6 =
	13		13

	2		5		5
sinβ =		*		=
	13		2		13

ICSP: Czy też na odwrót. Pytają o sinusy i je właśnie dostarczyliśmy.

fil: racja