funkacja wykładnicza parametr zosia: dla jakich wartości parametru m równanie |2^−2x−4−2|=m²−1 ma dwa rozwiązania jednakowych znaków? proszę o pomoc, bo nie wiem nawet jak się zabrać za to zadanie. Graficznie? Licząc z jakimiś warunkami?

ICSP: Graficznie Zaczynasz od narysowania f(x) = |2^{−2x − 4} − 2| potem tniesz go prostymi równoległymi do osi OX i patrzysz dla jakich wartości a zachodzą warunki zadania. Na koniec podstawiasz m² − 1 za a i rozwiązujesz nierówności/równania.

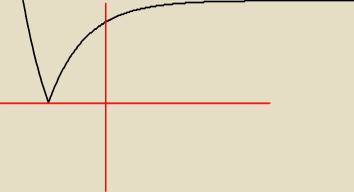
zosia: i w jaki spposb wyznaczyc te rozwiazania?

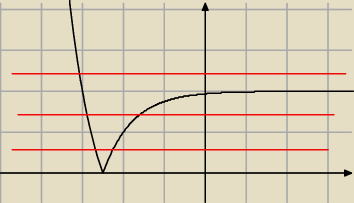
ICSP: teraz tniesz wykres prostymi równoległymi do osi OX. Takie proste mają równania: y = a musisz znaleźć takie a dla których pierwsza współrzędna punktów przecięcia z wykresem ma taki sam znak.

zosia: a>0 i a<2? oto chodzi?

ICSP: tak. Czyli 0 < a < 2 natomiast nasze równanie wygląda: |2^−2x−4−2| = a = m²−1 to pozostaje Ci rozwiązać: 0 < m² − 1 < 2

zosia: bardzo dziękuję za pomoc.

Bleee: ICPS −−− zapomniałeś o warunku, że oba rozwiązania mają mieć jednakowy znak więc

	1		31
|2−4 − 2| = |		− 2| =		<−−− to jest 'górna granica a'
	16		16

ICSP: a faktycznie. Uwierzyłem wykresowi, że przecina prostą x = 0 w punktcie (0;2) czyli :

	31
0 < a <
	16

co daje 0 < m² − 1 < U{31}[16} mój błąd.