dowod geometria
fil: Dany jest równoległobok ABCD . Okrąg wpisany w trójkąt BCD jest styczny do przekątnej BD w
punkcie L , a okrąg wpisany w trójkąt ABD ma środek S i jest styczny do boku AD w punkcie K
.
25 maj 21:08
Bleee:
coś Ci ucięło treść zadania

25 maj 21:09
Bleee:
pamiętaj że trójkąty BCD i ABD są przystające
25 maj 21:09
fil: Doklejam:
Wykaż, że jeżeli odcinek SL jest równoległy do prostej AB , to |KD | = |SL| .
25 maj 21:16
fil:
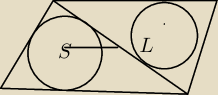
25 maj 21:17
fil:
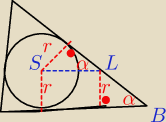
|SB| = |BL|
25 maj 21:22
Eta:
|SB|=|BL| ? ? bzdura !
25 maj 21:30
fil: |SL| = |LB|
25 maj 21:43
Eta:
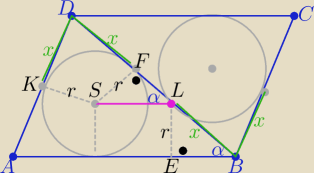
ΔEBL≡ΔSFL
to |SL|=|BL|=x =| KD|
25 maj 21:44


 |SB| = |BL|
|SB| = |BL|
 ΔEBL≡ΔSFL
to |SL|=|BL|=x =| KD|
ΔEBL≡ΔSFL
to |SL|=|BL|=x =| KD|