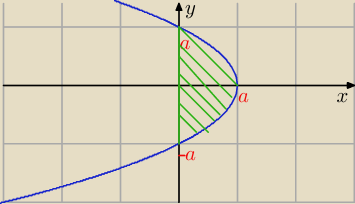
Pomocy! Oblicz całkę podwójną po wskazanym obszarze D: Marta2000: ∫∫_d ^dxdy_√ax−x² , (całka podwójna z dxdy przez pierwiastek z ax−x²) gdzie D jest obszarem ograniczonym parabolą y² = −ax + a² oraz osią OY Proszę o pomoc w rozwiązaniu przykładu. Wczoraj próbowałam poszukać jakiegoś podobnego, aby się wzorować i rozwiązać, niestety nie udało się. Jeśli jest taka możliwość to prosiłabym o rozpisanie kroków, a ja spróbowałabym je sobie po kolei wykonać.

piotr:

	1
∫−aa ( ∫0−y2/a+a		dx ) dy
	√ax−x2

Marta2000: Okej, a mogłabym się dowiedzieć skąd wiemy, że akurat trzeba tam wstawić kolejno: a, −a oraz y²/2a i 0, prosze? Podejrzewam, że w jakiś sposób rozwiązuje się to równanie paraboli. Potrzebuję komentarza jak to zrobić krok po kroku, bo chciałabym zrozumieć jak to zrobić, a nie się domyślać . Drugie pytanie, czy ktoś wie jak to zadanko wpisać w WolframAlpha? Z góry dziękuję za odpowiedzi i okazaną mi pomoc!

piotr: https://www.wolframalpha.com/input/?i=%E2%88%AB_%28-a%29%5Ea%28%E2%88%AB_0%5E%28-y%5E2%2Fa%2Ba%29%281%2F%28ax-x%5E2%29%5E%281%2F2%29%29dx%29dy

piotr: Czy umiesz narysować parabolę o podanym równaniu?

Marta2000: Przerysować parabolę wyżej potrafię, ale sama rozwiązać i narysować parabolę o takim równaniu nie wiedziałabym jak niestety.

Marta2000: Robię w ten sposób: y² = −ax+a² y² = a²−ax y² = a(a−x) y = √a √a−x lub y = − √a √a−x Ale nie wiem co mi to daje w sumie jak dalej tego użyć

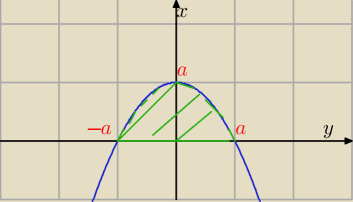
piotr: Możemy odpowiednio obrócić układ współrzędnych:

	y2
x = −		+ a
	a

	y2
x= 0 ⇔ −		+ a=0 ⇒ y=−a ∨ y=a
	a

W obszarze D

	y2
x zmienia się od 0 do −		+ a
	a

natomiast y zmienia się od −a do a stąd

	dx
∫−aa ( ∫		) dy
	√ax−x2

Marta2000: Okej, co teraz po kolei mam obliczyć? Najpierw zwykłą całkę ∫ ^dx_ax−x², ale co później bo już wszystko mi się pomieszało?

piotr: całka ma być taka:

	dx
∫−aa ( ∫0−y2/a+a		) dy
	√ax−x2

Marta2000: Wpisałam podaną całkę do wersji testowej programu mathematica, w którym zwrócony wynik to: 4√1/a² * a√a² Czy jest możliwość obliczenia "step−by−step" solution w tym programie? Nie potrafię sama jej obliczyć, WolframAlpha zwraca komunikat "Computation time exceeded", a chciałabym zobaczyć jak kroczek po kroku rozwiązać owy przykład.

Marta2000: Dobrze, rozumiem już jak obliczyliśmy te granice i skąd wziął nam się ostateczny wzór całki. Teraz jeszcze jakoś trzeba obliczyć tę całkę.

Marta2000: Jakiś pomysł jak obliczyć tę całkę? Mathematica dla a>0 wyświetla wynik 4a. Próbowałam obliczyć ale wychodzą mi wyniki typu ^{arcsin(−2y2/a−a)}_a − arcsin(−1). Ktoś wie jak tę całkę obliczyć poprawnie ?

ICSP: nic nie widać, ale proponuję najpierw całkowanie przez części w celu sprowadzenia arcsin(...) do funkcji wymiernej.

piotr:

1		1		2	1
	=		=
√ax−x2		√a2/4−(x−a/2)2		a	√1−((2x−a)/a)2

	2	1		2		a
∫			dx = (ze wzoru) =		arcsin((2x−a)/a)		+ C
	a	√1−((2x−a)/a)2		a		2

Marta2000: No dobrze, do tego momentu udało mi się dotrzeć, tam to 2/a i a/2 się skróci i wyjdzie sam arcsin(2x−a)/a + C, ale po podstawianiu granic gubię się i wychodzą mi nieciekawe wyniki.

Marta2000: arcsin((2x−a)/a) + C*

Marta2000: Jak się podstawia pod X "a" to wychodzi mi arcsin(a)/a czyli −1. I teraz mam problem, nie wiem co dalej.