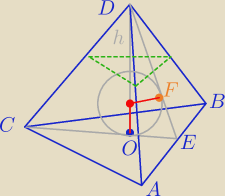
Czworościan i kula w niego wpisana Shizzer: W czworościanie, którego wszystkie krawędzie mają taką samą długość 6, umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna π, równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości

	8
równej		objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka S
	27

kuli od płaszczyzny π, tj. długość najkrótszego spośród odcinków SP, gdzie P jest punktem płaszczyzny π.

	2
Do rozwiązania tego zadania brakuje mi tylko zrozumienia dlaczego |DF| =		|DE|. Mógłby
	3

mi ktoś wyjaśnić z czego to wynika? Wiem, że skala podobieństwa mniejszego ostrosłupa, którego podstawą jest przekrój π do większego

	2		2
ostrosłupa to k =		, ale to raczej nic nie wnosi do tego, że |DF| =		|DE|
	3		3

Qulka: bo to punkt styczności kuli ,,, taki sam jak na dole a spodek wysokości jest w h/3 i 2h/3

Shizzer: Rozumiem. Bardzo dziękuję

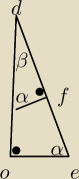
fil: z podobnienstwa tych trojkatow

Qulka: albo szybciej że OE=EF bo styczne do kuli

Shizzer: Zrobiłem z podobieństwa trójkątów. Właśnie do tego podobieństwa brakowało mi tego jednego odcinka