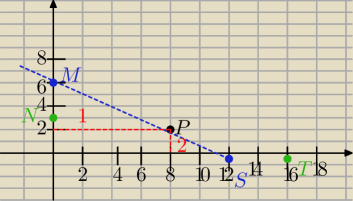
geometria salamandra: Prosta l na której lezy punkt P=(8,2) tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej l. Podzieliłem to na prostokąt i dwa trójkąty podobne P_prostokąta=16 M=(0, 2+w) S=(t+8, 0)

	8*w
P1=		=4w
	2

	2*t
P2=		=t
	2

P₁₊₂=20 4w+t=20 t=20−4w Z podobieństwa trójkątów 1 i 2

t		2
	=
8		w

20−4w		2
	=
8		w

20w−4w²=16 −4w²+20w−16=0 / : 4 −w²+5w−4=0 Δ=25−16=9

	−5−3
w1=		=4
	−2

	−5+3
w2=		=1
	−2

1) M=(0,6) t=20−16=4 S=(12,0) 2)N=(0,3) T=(16,0) 1) 6=b 2=8a+b 2=8a+6 8a=−4

	1
a=−
	2

	1
y=−		x+6
	2

2) 3=b 2=8a+b 2=8a+3 8a=−1

	1
a=−
	8

	1
y=−		x+3
	8

Dwie proste wyszły, jest ok sposób w ogóle?

Qulka: a nie prościej y=ax+b b=2−8a P_Δ=b•(−b/a)/2 i podstawić?

salamandra: zaraz spróbuję i powiem

jc: A może tak? Przyprostokątne: a, b. Równie prostej: x/a+y/b=1. ab/2 = 36 8/a + 2/b=1 ab=72 8b+2a=ab=72 a+4b=36 (36−4b)b=72 b²−9b+18=0, b=6 lub b=3 (a=12 lub a= 24 odpowiednio) Mamy dwie takie proste: x/12 + y/6=1, x/24+y/3=1 Inaczej: x+2y=12, x+8y=24.

salamandra:

	x		y
@jc, wybacz, może głupie pytanie, ale skąd jest		+		=1?
	a		b

Jerzy: To tzw. równanie odcinkowe prostej.