analiza stunks:

	5
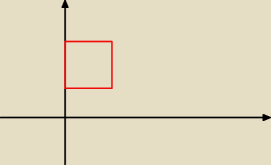
Przypuśćmy, że to obszar [0,		] x [1, 3] i mamy funkcję f(x, y) = x + y.
	2

Jak wygląda infimum na prostokątach w podziale tego obszaru?

	52		2
P = {(xi, yj): Δxi =		, Δyj =		}
	25		20

Chodzi o to, że konstruuję sumę dolną Darboux ∑∑m_ij*Δp_ij, gdzie m_ij jest infimum na zbiorze p_ij ← czyli prostokącie i zastanawiam się, czy dobrze to robię. Powinienem jako

	i		j
infimum przyjąć f(		, 1 +		)?
	25		20

Tylko czy suma ta nie powinna być mniejsza niż pole obszaru?