Funkcja, parametr Szkolniak:

	x3
Dla jakich wartości parametru m funkcja f(x)=		jest określona i rosnąca na
	mx2+6x+m

całej prostej rzeczywistej? Tak jak z określonością nie mam problemu, tak nie do końca jestem pewien co z drugim etapem w poleceniu. Dobrze rozumiem, że muszę sprawdzić dla jakich m f'(x)>0 dla x∊ℛ?

fil: Wedlug mnie tak, tez bym tak zrobil

Jerzy: Tak,ale co oznacza „ prostej rzeczywistej” ?

Szkolniak: Co prawda pierwszy raz spotkałem się z takim określeniem, ale na pierwszy rzut oka zrozumiałem to jako zbiór liczb rzeczywistych, bez żadnych ograniczeń − prawidłowo?

Jerzy: Nie ma takego pojęcia,jak prosta rzeczywista,a tym bardziej dziedzina.

Jerzy: Skąd to zadanie ?

fil: Jest − inaczej os liczbowa, google nie gryzie

Jerzy: Najwyraźniej jestem niedouczony

Szkolniak: 'Korespondencyjny Kurs z Matematyki'

	2x3[mx2+(6−m)x+m−3)]
Doszedłem do postaci f'(x)=		.
	(mx2+6x+m)2

Dla odpowiednio określonego 'm' mianownik jest dodatni dla x∊R, zatem rozpatrujemy tylko taką nierówność: 2x³[mx²+(6−m)x+m−3)]>0 W takim razie czy z tego nie wynika, że nieważne jakie 'm' obierzemy, to i tak dana nierówność nigdy nie będzie prawdziwa?

fil: a to ciekawe, x⁵ jako najwzysza potega

fil: f'(x) − licznik wynosi x²(mx² + 12x + 3m)

Jerzy: No i klapa, bo pochodna nie jest stale dodatnia.

Minato: Dlaczego? Przecież należy wyznaczyć takie m, aby funkcja f była określona i rosnąca na R

Szkolniak: Rzeczywiście, w zeszycie teraz widzę błąd na początku − pochodna z x³ zapisana jako 2x³.

	x2(mx2+12x+3m)
W takim razie f'(x)=		− czy w takim razie z tego również nie
	(mx2+6x+m)2

wynika to, że nie istnieje taki parametr m?

fil: mx² + 12x + 3m > 0 m > 0 && Δ < 0 Δ = 144 − 12m² < 0 12 − m² < 0 m² > 12

Jerzy: @Minato,nie widzisz,że pochodna ma miejsce zerowe ?(zakładam,że jest dobrze policzona)

Szkolniak: Dobrze policzona, mi i filowi wyszły takie same Podsumowując − taka wartość parametru m nie istnieje?

fil: @Jerzy i co z tego Zapewne chodzi o >= a nie o >

Jerzy: Przedobrzyłem,bo w zerze może być punkt przegięcia.

Szkolniak: Czyli dopuszczamy równość? I w takim razie czy to nie jest kwestia interpretacyjna? Jeśli nie − jaka i gdzie byłaby ta różnica mówiąca nam, że mamy obrać znak '≥', a nie akurat '>'?

Minato: jak dla mnie, rozwiązanie istnieje i jest to zbiór m > √12

Szkolniak: No ciekawe, bo gdy weźmiemy pierwsze m naturalne spełniające daną nierówność (m=4), wtedy nasza

	x3		4x2(x2+3x+3)
funkcja f(x)=		→ f'(x)=		.
	4x2+6x+4		(4x2+6x+4)2

Pytanie jak w takim momencie powinniśmy potraktować ten punkt x=0?

fil: 0 jest pierwiastkiem dwukrotnym, wiec wykres sie "odbije"

Szkolniak: Racja.. Swoją drogą − zastanawiałem się kiedyś nad taką sytuacją: Przyjmijmy, że mamy za zadanie znaleźć ekstrema lokalne funkcji określonej na zbiorze liczb ℛ i mamy już policzoną pochodną funkcji i rozłożoną na czynniki. Następnie przyrównujemy pochodną do zera i tworzy nam się zbiór kandydatów. W dalszej kolejności oczywiście rozwiązujemy nierówności f'(x)>0 i f'(x)<0, aby przekonać się czy na pewno w danych punktach istnieje maximum bądź minimum. Teraz pytanie − czy można powołać się na krotność danego pierwiastka (powiedzmy, że dany pierwiastek jest nieparzystej krotności) i na tej podstawie stwierdzić że następuje tam zmiana znaku − co równa się z istnieniem ekstremum?

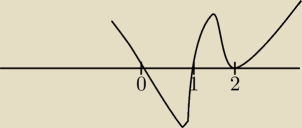
fil: Jak juz do tego dochodzisz, polecam narysowac przyblizony wykres wielomianu w liczniku. Nastepnie wiesz, ze pierwiastek z parzysta krotnoscia "odbije" sie od osi ox, natomiast pierwiastek z nieparzysta krotnoscia przejdzie dalej. Przykladowo wezmy cos takiego: x³(x − 2)²(x − 1)

fil: Nie jestem jakims dobrym rysownikiem

Szkolniak: O tym mówię i zdaję sobie sprawę, że parzysta krotność odbija, a nieparzysta przebija Pytanie czy powiedzmy na maturze byłoby to maksymalnie zapunktowane, jeśli zamiast badania f'(x)>0 i f'(x)<0 powiedziałbym o krotności pierwiastka − czy jest to wystarczający dowód na to, że wtedy istnieje ekstremum?

fil: Tak, jednak jesli pytaja nas konkretnie o maximum/minimum to fajnie pokazac na wykresie, ze pochodna zmienia znak oraz dodac komentarz

fil: Bo niestety od ktoregos tam roku trzeba dawac komentarz....jesli go nie dasz − odejmuja punkt

Szkolniak: W sumie racja, co szkodzi machnąć na szybko na boku rysunek i zaznaczyć jak to mniej więcej wygląda. No nic, dzięki wielkie za rozwiązanie wątpliwości