stereometria , obrót trójkąta
dzejbi: Dany jest trójkąt ABC w którym |<BCA|=α ,|<BAC|=β oraz |<ABC|>90°
Promień okręgu opisanego na tym trójkącie ma długość R. Trójkąt
obracamy wokół boku BC. Oblicz objętość otrzymanej bryły obrotowej.
próbuje to robić ale nie wychodzi
wiem ze obrót takiej bryły to złączone podstawą stożki , jak sobie radzić przy tego typu
zadaniach?
23 maj 17:48
Mila:
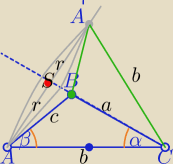
|SC|=H − wysokość dużego stożka
|SB| − wysokość małego stożka
1)
r=b*sinα
b − oblicz z tw. sinusów
2) |SB|=|SC|−a
| | 1 | |
3) V figury= |
| *[πr2*|SC|−πr2*|SB| ]= |
| | 3 | |
| | 1 | | 1 | |
= |
| πr2*[ |SC|−(|SC|−a)]= |
| πr2*a |
| | 3 | | 3 | |
a− oblicz z tw. sinusów
23 maj 18:43
a7:
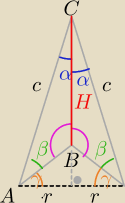
jest to stożek w środku z "wyżłobionym" stożkiem, którego objętość trzeba odjąć od pierwszego
23 maj 18:49
 |SC|=H − wysokość dużego stożka
|SB| − wysokość małego stożka
1)
|SC|=H − wysokość dużego stożka
|SB| − wysokość małego stożka
1)
 jest to stożek w środku z "wyżłobionym" stożkiem, którego objętość trzeba odjąć od pierwszego
jest to stożek w środku z "wyżłobionym" stożkiem, którego objętość trzeba odjąć od pierwszego