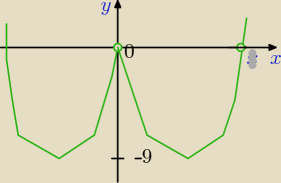
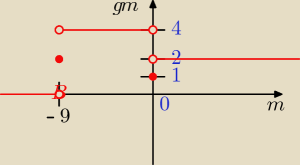
zad matthew: Cześć, mam takie zadanie: Na podstawie wykresu odpowiedniej funkcji podaj liczbę rozwiązań równania |x² − 6x| = m w zależności od parametru m. Narysuj wykres funkcji g(m) przyporządkowującej liczbom m liczbę rozwiązań danego równania. Zarobiłem tak: |x² − 6x| = m x² − 6x ≠ 0 x(x−6) ≠ 0 x ≠0 x≠ 6 1 rozw. dla m = {0} 2 rozw. dla m ∊ {−9}∪ (0; + ∞) 4 rozw. dla m ∊ (−9; 0) 0 rozw. dla m ∊ (−∞; − 9) { 1 rozw. dla m = {0} { 2 rozw. dla m ∊ {−9}∪ (0; + ∞) g(m) ={ 4 rozw. dla m ∊ (−9; 0) { 0 rozw. dla m ∊ (−∞; − 9)

matthew: bardzo prosze o sprawdzenie...

Noah: jesli f(x)=|x²−6x| to m jest prosta o rownaniu y=m tak mysle a wiec troche by inaczej bylo z tego co widze dales x=m ale nie wiem czy dobrze

Godzio: cos namotane zaraz pomoge

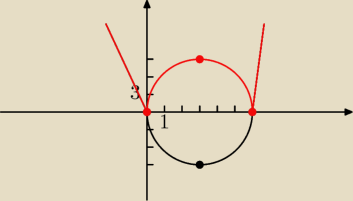
Godzio: rysujemy sobie wykres f(x) = x² − 6x miejsca zerowe: x(x−6) => x=0 v x=6 p = 3

	−36
q =		= −9
	4

i odbijamy dolną część względem OX teraz na bazie czerwonego wykresy f(x) = |x²−6x| sprawdzamy te rozw. 0 rozw. dla m∊(−∞,0) 2 rozw. dla m∊(9,∞) ∪ {0} 3 rozw. dla m = 9 4 rozw. dla m∊(0,9) i teraz ten wykres f(m) który już chyba zrobisz poprawnie nie rozumiem jeszcze dlaczego x²−6x ≠ 0

matthew: no wlasnie jak to jest... gdy y = |f(x)| − to znaczy, ze odbija symetrycznie ujemna czesc wykresu a y = f(|x|) − likwiduje lewa czesc, a na to miejsce odpija symetrycznie prawą część ale w takim razie ta podana funkcja to nie jest y = f(|x|) ? no bo zawsze wydawało mi sie, ze aby zastosować tą pierwsza własność, funkcja musi wyglądać tak: |f(x) = x² − 6x| czy moze ja bralem to zbyt doslownie? tzn, ze finkcja musiala by wyglądać tak: f(x) = |x²| − 6x aby zastosować tą drugą własność? dzieki za odpowiedzi

Godzio: zbyt dosłownie aby było tak jak ty mówisz to by musiało być : f(x) = x² − 6|x|

matthew: no wlasnie bezsensu... zaczałem liczyć dziedzine

matthew: aha ok dzieki

matthew: jest takie zdanie: Dany jest wielomian P(x) = (x−2)(x−m−5)(x−6m−20) a) podaj pierwiastki tego wielomianu b) wyznacz paametr m, tak aby wielomian mial dokladnie dwa pierwiastki. a) P(x) = (x−2)(x−m−5)(x−6m−20) D(x) = x − 2 ⇒ x = 2 P(2) = 6m² + 36m + 54 Δ = 0 a₀ = −3 P(x) = (x−2)(x+3−5)(x+18−20) P(x) = (x−2)(x−2)(x−2) x = 2 proesze o sprawdzenie punktu a) z punktem b) nie wiem co zrobic.... prosze o mała podpowiedz

Godzio: pierwiastki wielomianu: x = 2 x = m+5 x = 6m − 20 b) żeby wielomian miał dwa pierwiastki to (x−m−5)(x−6m−20) musi mieć jeden pierwiastek: W(x) = x² − 6mx −20x −mx +6m² +20m −5x +30m + 100 W(x) = x² −25x − 7mx +6m² + 50m + 100 W(x) = x² + x(−25−7m) +6m² + 50m + 100 zał. Δ = 0 Δ=625 + 350m + 49m² −24m² −200m − 400 = 25m² + 150m − 225 = 0 25m² + 150m − 225 = 0 m² + 6m − 9 = 0 (m−3)² = 0 m = 3

matthew: Godzio pomyliles sie w rachunkach... Δ = m² + 6m + 9 i m = −3 ale to tak samo jak mnie wyszlo kiedy obliczalem m..... i kiedy za m podstawie − 3 wcale nie wychodza dwa pierwiastki tylko jeden, zerknij na gore Dzieki za odpowiedz

Godzio: mój bład wynika z tego że 625 − 400 = + 225 więc 25m² + 150m + 225 m² + 6m + 9 = 0 (m+3)² = 0 m = −3 x₁= 2 x₂= −3 + 5 = 2 x₃ = 18 − 20 = −2 czyli pierwiastkami są x₁ = 2 i x₂ = −2 W(x) = (x−2)² * (x+2)