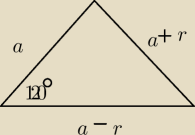geometria salamandra: Długości boków trójkąta ABC są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę 120 stopni. Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta ABC jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu. a−r, a, a+r − boki trójkąta z Tw. cosinusów: a²+2ar+r²=a²+a²−2ar+r²−2a(a−r)*cos120

	1
a2+2ar+r2=2a2−2ar+r2−(2a2−2ar)*(−		)
	2

a²+2ar+r²=2a²−2ar+r²+a²−ar a²+2ar+r²−2a²+2ar−r²−a²+ar=0 −2a²+4ar+ar=0 −2a²+5ar=0 a(−2a+5r)=0 a=0 v 5r=2a

	5
a=		r
	2

	5		5		5
Vprostopadłościanu= (		r−r)*		r*		r+r)
	2		2		2

	3		5		7
V=		r*		r*		r=U{105}{r3
	2		2		2

105
	r3=840
8

105r³=6720 r³=64 r=4

	5
a=		*4=10
	2

6,10,14− boki trójkąta R− promień kuli R=6

	4
V=		π*63=288π
	3

Pierwsze pytanie− czy dobrze, a drugie pytanie/wątpliwość czy mogłem założyć, że ten kąt 120 stopni jest naprzeciwko boku a+r (założyłem, że jest to ciąg rosnący o r dodatnim), ale zastanawiam się, co by było, jakby to był malejący ciąg, wtedy ten kąt powinien leżeć naprzeciwko kąta a−r. Czy wtedy po prostu boki trójkąta wyszłyby w kolejności 14,10,6 i byłoby to to samo

wredulus_pospolitus: drugie pytanie −−− tak ... mogłeś to przyjąć (ale dobrze by było wiedzieć dlaczego to przyjąć można ) otóż kąt o największej mierze będzie naprzeciw najdłuższego boku (tw. sinusów się kłania ) ... związku z tym, że 120^o to kąt rozwarty, więc wiemy że w tymże trójkącie będzie to kąt o największej mierze, więc na przeciw niego będzie bok 'a+r'. zapisując boki: a−r , a , a+r bez utraty ogólności możesz przyjąć r ≥ 0

salamandra: @wredulus, wiem, że naprzeciw największego boku jest największy kąt, natomiast moje pytanie tyczyło się, że gdyby to był ciąg malejący (tj. r<0), wtedy najdłuższym bokiem byłby a−r