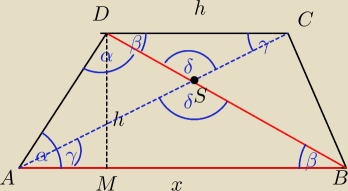
planimetria salamandra: W trapezie równoramienmym ABCD dłuższa podstawa AB ma taką samą długość jak jego przekątna BD, a długość krótszej podstawy CD jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu .

	x+h
MB=
	2

AB=x DM=h

	x+h
W ΔMDB: (		)2+h2=x2
	2

x2+2xh+h2
	+h2=x2 / * 4
4

x²+2xh+h²+4h²=4x² 5h²=3x²−2xh

	3x2−2xh
h2=
	5

Próbowałem wszelakimi sposobami, ale nie wiem jak uzaleznić "h" od x, żeby coś podziałać dalej....

ICSP: 5h² = 3x² − 2xh : // h² > 0

	x		x
5 = 3(		)2 − 2
	h		h

fil: Mozna tez tak: 5h² + 2xh − 3x² = 0 Δ = 4x² + 60x² = 64x²

	−2x − 8x
h1 =		< 0
	10

	−2x + 8x		3
h2 =		=		x
	10		5

i dalej juz prosto

Minato:

	2a+2b
|AE| =		= a+b
	2

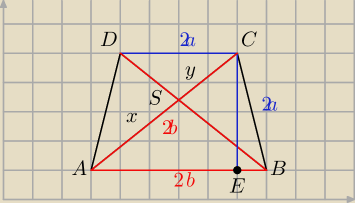
ΔAEC jest prostokątny zatem z tw. Pitagorasa (2b)² = (a+b)² + (2b)² ... ΔASB ~ ΔDSC (kkk)

2a		y
	=
2a		x

salamandra: Nie wiedziałem, że mogę to potraktować jako równanie kwadratowe.... dzieki, zaraz spróbuje dokończyć

salamandra:

x		AS
	=
h		CS

	3
x*CS=		x*AS
	5

	3
CS*x=AS*		x / : x
	5

	3
CS=U{AS*		x}}{x}
	5

	3
CS=		AS
	5

więc stosunek 2:3?

Minato: 4a² = a²+2ab+b²+4b² 3a² − 2ab − 5b² = 0 | :b²

	a		a		a
3(		)2 − 2		− 5 = 0		=t
	b		b		b

3t − 2t − 5 = 0 Δ = 4+60 =64

	2−8
t1 =		< 0 n.s.w.z.
	6

	2+8		3
t2 =		=
	6		5

a		3		y
	=		=
b		5		x

skąd Ci się wzięło 2:3?

salamandra: Skoro "całość" ma "5", i AS=3, a CS=2, no to w stosunku 2:3 / 3:2 się dzielą (zawsze mi się to myli, sprostuj)

Minato:

	CS		3
Twój rysunek, szukasz		, a masz wyliczone CS =		AS, czyli
	AS		5

	CS		3
po podzieleniu przez AS masz		=
	AS		5

Ogólnie, jak masz np. podany stosunek a:b jest równy 7:2, oznacza, że a+b ma długość (7+2)x = 10x (x jest ważny, bo nie jest istotne czy to będę metry czy centymetry). Teraz a = 7x oraz b = 2x

salamandra: Ja rozumuję to tak: jeżeli dzielimy ciasto na 5 kawałków i dostajemy je w proporcjach 2:3, to znaczy, że ja dostaję dwa kawałki, a Ty trzy

salamandra:

	3
Ok, a można powiedzieć, że CS=		CAŁEJ przekątnej?
	8

annabb: tak

Minato: tak

salamandra: W takim razie rozumiem, pomyliło mi się− przecież my wyliczyliśmy stosunek odcinka do odcinka, a nie do całej przekątnej, dzięki