Dżiometrikal probelm
FiF: Udowodnij, że w czworokącie odległości między środkami przeciwległych boków są równe
wtedy i tylko wtedy, gdy przekątne tego czworokąta są prostopadłe.
22 maj 17:44
FiF: bump
22 maj 18:14
wredulus_pospolitus:
bump chociaż rysunek zrobił

22 maj 18:15
FiF:
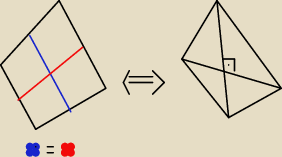
Te dwa czworokąty to tak naprawdę ten sam czworokąt, tylko nie mam talentu artystycznego.
22 maj 18:20
FiF: Czerwony i niebieski odcinek to jest odległość od środków przeciwległych boków w czworokącie
22 maj 18:22
wredulus_pospolitus:
Widzę że bump nie zrozumiał.
Nie pytałem się czy potrafisz narysować tutaj na forum, tylko czy chociaż w zeszycie
narysowałeś/−aś.
Chce sprawdzić co w ogóle udało Ci się zrobić, jaki tok myślenia zrobiłeś/−aś.
Czy udowodniłeś/−aś jedną ze stron, czy żadnej.
22 maj 18:23
FiF: Żadnej niestety. Nie mam pomysłu na to zadanie, więc pytam tutaj
22 maj 18:26
ABC:
masz to udowodnić w sposób jaki?
− aksjomaty Euklidesa
−rachunek wektorowy
−geometria analityczna
czy wolna amerykanka wszystkie chwyty dozwolone?
22 maj 20:48
22 maj 21:45
RubikSon: wolna amerykanka
22 maj 22:19
Iks: FiF=RubikSon a to w linku nie wystarczy?
22 maj 23:18
ABC:
w jedną stronę jest dość prosty dowód z normalnej geometrii
22 maj 23:44
Eta:
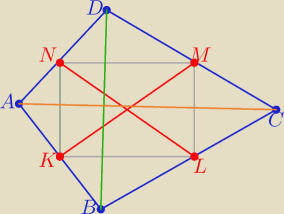
1/jeżeli |KM|=|NL| to czworokąt KLMN jest prostokątem lub kwadratem
bo przekątne kwadratu i prostokąta mają równe długości
2/ zatem NK⊥NM i NK∥BD i NM ∥ AC ⇒ AC⊥BD
c.n.w.
23 maj 19:10
Mila:
I jeszcze dodałabym na początku:
Odcinki łączące środki boków przeciwległych dowolnego czworokąta wypukłego przecinają się
w punkcie dzielącym te odcinki na połowy.
23 maj 21:23
Eta:

23 maj 22:31

 Te dwa czworokąty to tak naprawdę ten sam czworokąt, tylko nie mam talentu artystycznego.
Te dwa czworokąty to tak naprawdę ten sam czworokąt, tylko nie mam talentu artystycznego.
 1/jeżeli |KM|=|NL| to czworokąt KLMN jest prostokątem lub kwadratem
bo przekątne kwadratu i prostokąta mają równe długości
2/ zatem NK⊥NM i NK∥BD i NM ∥ AC ⇒ AC⊥BD
c.n.w.
1/jeżeli |KM|=|NL| to czworokąt KLMN jest prostokątem lub kwadratem
bo przekątne kwadratu i prostokąta mają równe długości
2/ zatem NK⊥NM i NK∥BD i NM ∥ AC ⇒ AC⊥BD
c.n.w.
