dowody algebraiczne
m:
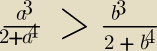
Wykaż, że jeżeli a<b≤−2, to (rysunek)
22 maj 09:59
Minato:
Pokaż, że funkcja określona wzorem
jest malejąca w przedziale (−
∞; −2)
22 maj 10:16
n: A można wiedzieć dlaczego taki wniosek?
22 maj 10:24
Minato:
1) zauważmy, że wyrażenia po prawej i lewej stronie nierówności różnią się tylko
| | x3 | |
zmienną, czyli są budowane wg schematu |
| = f(x). |
| | 2+x4 | |
2) mamy podany warunek a < b ≤ −2 (inaczej mówiąc, a jest mniejsze niż b)
3) mamy pokazać, że f(a) > f(b)
(w języku funkcji oznacza to, że dla argument a, przyjmujemy większe wartości niż
dla argumentu b), czyli a < b ⇒ f(a) > f(b) − definicja funkcji malejącej.
22 maj 10:31
n: Dobra czyli muszę udowodnić, że f'(x) dla x < −2 przyjmuje wartości ujemne
−x
2(x
4−6)=0
x=0 v x
4=6
x = {−
√6, 0,
√6} − pierwiastki 4 stopnia
Rysuję wykres...
Czyli f'(x)<0 dla x<−
√6
| | √6 | | √6 | |
Liczę f(√6)= |
| = |
| =0.3 |
| | 2+6 | | 8 | |
I się pogubiłem już
22 maj 11:33
Minato:
| | 3x2(2+x4)−x3*4x3 | | −x6+6x2 | |
f'(x) = |
| = |
| < 0 |
| | (2+x4)2 | | (2+x4)2 | |
−x
6+6x
2 < 0
x
2(6−x
4) < 0
x =0 x = −
4√6 x =
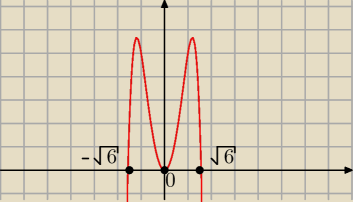
4√6 (na rysunku g(x) = −x
6+6x
2)
f'(x) < 0 ⇔ x ∊ (−
∞, −
4√6) ∪ (
4√6, −
∞) → f'(x) maleje w (−
∞, −
4√6) oraz (
4√6, −
∞)
−
4√6 > −2, zatem f maleje na pewno w przedziale (−
∞, −2).
Dla a < b < −2 mamy f(a) > f(b), czyli
22 maj 12:17
n: Dziękuję za poświęcenie
22 maj 12:34
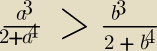 Wykaż, że jeżeli a<b≤−2, to (rysunek)
Wykaż, że jeżeli a<b≤−2, to (rysunek)
