Rozwiąż równanie sin6x+cos3x=2sin3x+1 w przedziale ⟨0,π⟩. Opeus: Rozwiąż równanie sin6x+cos3x=2sin3x+1 w przedziale ⟨0,π⟩. Próbuję to zrobić z sinusa podwojonego kąta: sin3*2x +cos3x=2sin3x+1 2sin3x cos3x = 2sin3x+1 cos3x(2sin3x+1)−(2sin3x+1)=0 (cos3x−1)(2sin3x+1)=0

	1
cos3x=1 v sin3x=−
	2

czy teraz koniecznie muszę podstawić za 3x = t czy jest inna droga?

a7: cos3x=cos(2kπ) 3x=2kπ x=2/3kπ lub sin3x=−1/2 sin3x=sin(π/4+2kπ) x=π/12+kπ/6 chyba tak można ?

Flo: Nie.

	π		5π
3x=2kπ lub 3 x=π+		+2kπ lub 3x=π+		+2kπ /:3
	6		6

	2π		7π		2kπ		11π		2kπ
x=		lub x=		+		lub x=		+
	3		18		3		18		3

teraz podstaw k=0 i k=1 i te wybierasz rozw, które należą do podanego przedziału

Opeus: Kurde, nie rozumiem dlaczego podstawiamy 3x=2kπ. Przecież to ma się nie powtarzać bo D: ⟨0,π⟩. Odpowiedzi do tego zadania to:

	7		11		2
x∊{		π,		π,		π, 0}
	18		18		3

Sorry, ale tępy jestem.

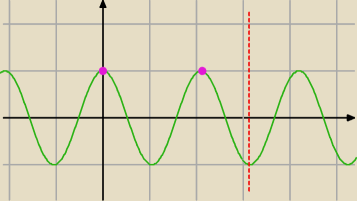
a7: cos3x=1

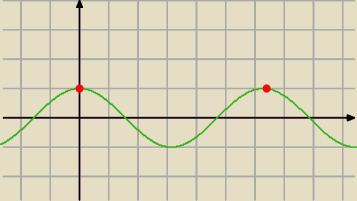
a7: cosx=1 dla x=2π dlatego cos3x=cos(2π) 3x=2π czyli x=2π/3 ponieważ okres cos3x jest trzy razy "częstszy" T=2π/3 to w przedziale <0,π> będzie 0 i 2π/3 rozwiązaniem tej części równania

annabb: bo jak masz jakąś liczbę przed x to jak podzielisz to te powtórzenia się zacieśnią i więcej się załapie w badanym kawałku

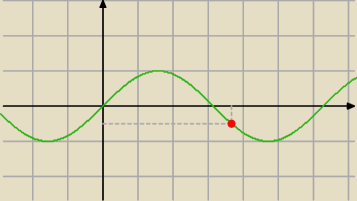
a7: jeśli chodzi o sin3x=−1/2 to tak samo sinx=−1/2 dla x=7π/6+2π/3 3x=7π/6 x=7π/18+4π/9 czyli x=7π/18 lub x=11π/18 ( w tym przedziale tylko te dwa rozwiązania dla tej części równania)

annabb: poza tym czasem trzeba przesunąć rozwiązania, bo masz je podać w innym zakresie i wtedy też się przydaje kπ

a7: chochlik sinx=−1/2 dla x=7π/6, a T sin3x=2π/3=4π/9, więc 3x=7π6+4π/9 czyli x=7π/18 lub x=11π/18 trochę pogmatwałam, sorki

Mila: Podstaw k=0 wtedy otrzymasz :

	7π		11π
x=0 lub x=		lub x=
	18		18

k=1

2π

7π

2π

7π

12π

19π

x=

∊<0,π>lub x=

+

=

+

=

>π

3

18

3

18

18

18

	2π		7π		11π
odp. x∊{0,		,		,		}
	3		18		18