AS:
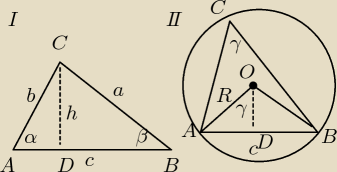
Rysunek I
| | h | | h | |
ΔACD: |
| = sin(α) ΔBCD: |
| = sin(β) |
| | b | | a | |
h = b*sin(α) h = a*sin(β)
Porównując h z obu rwności
a*sin(β) = b*sin(α) stąd
Podobnie postępując z bokami b i c otrzymamy
| a | | b | | c | |
| = |
| − |
| |
| sin(α) | | sin(β) | | sin(γ) | |
Druga część twierdzenia (rys. II)
Kąt AOB jest dwukrotnie większy od kąta ACB jako kąt środkowy
wsparty na tym samym łuku co kąt wpisany
Z Δ AOD mamy
| c/2 | | c | |
| = sin(γ) ⇒ c = 2*R*sin(γ) lub |
| = 2*R |
| R | | sin(γ) | |
Ostatecznie:
| a | | b | | c | |
| = |
| − |
| = 2*R |
| sin(α) | | sin(β) | | sin(γ) | |
