W 33-osobowej klasie
Michal: W 33−osobowej klasie wszyscy uczą się któregoś z języków: włoskiego, hiszpańskiego lub
portugalskiego.
Wśród 15 uczniów uczących się języka portugalskiego, 7 osób uczy się także języka włoskiego, 6
hiszpańskiego, a 2 wszystkich trzech języków.
Ile osób uczy się wyłącznie języka włoskiego, jeśli wiadomo, że osób uczących się włoskiego
jest tyle samo, co osób uczących się języka hiszpańskiego, a obu tych języków uczy się 5 osób?
20 maj 15:12
Minato:
W − uczniowe uczący się włoskiego
H − uczniowie uczący się hiszpańskiego
P − uczniowie uczący się portugalskiego
|W ∪ H ∪ P| = |W| + |H| + |P| − |W ∩ H| − |W ∩ P| − |H ∩ P| + |W ∩ H ∩ P|
i dalej sam
20 maj 15:19
Michal: próbowałem tak robić jednak wychodzą mi złe liczby i nie wiem gdzie popelniam błąd
20 maj 15:20
Minato:
|W ∪ H ∪ P| = 33
|P| = 15
|P ∩ W| = 7
|P ∩ H| = 6
|W ∩ H ∩ P| = 2
|W| = |H| = x
|W ∩ H| = 5, zatem
33 = 15 + x + x − 7 − 6 − 5 + 2
2x = 34
x = 17
20 maj 15:38
Minato:
a nie, czekaj
20 maj 15:39
wredulus_pospolitus:
Michał −−− to pokaż jak liczysz
20 maj 15:43
a7:
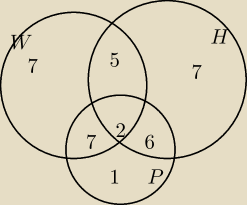
Odp. 7
20 maj 15:44
a7: 
(nie wiem czy na pewno ok)
20 maj 15:45
wredulus_pospolitus:
a7 −−− ja bym polemizował
"obu tych języków uczy się 5 osób" <−−−− oznacza że 5 osób uczy się zarówno włoskiego jak i
hiszpańskiego (co nie oznacza, że nie może się uczyć portugalskiego).
20 maj 15:46
wredulus_pospolitus:
Druga sprawa −−− liczba osób ucząca się włoskiego jest u Ciebie różna od liczby osób uczących
się hiszpańskiego
20 maj 15:47
a7:
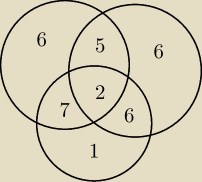
przepraszam powinno być wg mnie 6
20 maj 15:47
Minato:
Niech |P| = y oraz |W| = |H| = x, wówczas
2x + y = 13
2x = 13 − y
y musi być nieparzysty, zatem
y ∊ {1, 3, 5}
i sprawdzasz jakie mogą być x, aby klasa liczyła 33 osoby
20 maj 15:48
a7: tak już widzę błąd
20 maj 15:49
a7:
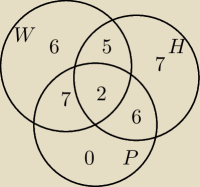
odp. 6
20 maj 15:50
wredulus_pospolitus:
Saizou −−− a skąd równanie 2x + y =
13 
Druga sprawa
Jakim cudem 2x + y = 13 w momencie w którym klasa liczy sobie 33 osoby, a
|P| −−− liczba osób uczących się portugalskiego (nie liczba osób uczących się JEDYNIE
portugalskiego)
Jeżeli zastosujesz, że |P|, |W| i |H| to liczba uczniów uczących się JEDYNIE danego języka, to
założenie, że |W| = |H| jest nadinterpretacją

20 maj 15:52
a7: 
20 maj 15:52
wredulus_pospolitus:
@a7 −−− nadal −−− liczba uczniów uczących się zarówno włoskiego jak i hiszpańskiego wynosi 5 +
2 = 7, co jest sprzeczne z treścią zadania: " obu tych języków uczy się 5 osób"
20 maj 15:54
wredulus_pospolitus:
analogicznie −−−− napisane jest:
wśród 15 uczniów uczących się portugalskiego,
7 uczy się także włoskiego (co nie znaczy że się nie uczą także hiszpańskiego),
6 uczy się także hiszpańskiego (co nie znaczy że się nie uczą także włoskiego),
2 uczy się wszystkich trzech języków
Czyli;
|P n W n H| = 2
|P n W| − |P n W n H| = 5
|P n H| − |P n W n H| = 4
a także:
|W n H| − |P n W n H| = 3
20 maj 15:57
Minato:
żle zrozumiałem treść zadania.
20 maj 16:04
a7:
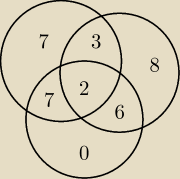

może teraz ok?
20 maj 16:15
wredulus_pospolitus:
@a7 −−− patrz co napisałem o 15:57

20 maj 16:18
wredulus_pospolitus:
15 + (2x+1) + 3 = 33 −−−> 2x = 14 −> x = 7
ale diagram troszeczkę inaczej będzie wyglądał (tylko portugalskiego uczyć się będzie w sumie 4
uczniów)
20 maj 16:20
 Odp. 7
Odp. 7
 (nie wiem czy na pewno ok)
(nie wiem czy na pewno ok)
 przepraszam powinno być wg mnie 6
przepraszam powinno być wg mnie 6
 odp. 6
odp. 6
 Druga sprawa
Jakim cudem 2x + y = 13 w momencie w którym klasa liczy sobie 33 osoby, a
|P| −−− liczba osób uczących się portugalskiego (nie liczba osób uczących się JEDYNIE
portugalskiego)
Jeżeli zastosujesz, że |P|, |W| i |H| to liczba uczniów uczących się JEDYNIE danego języka, to
założenie, że |W| = |H| jest nadinterpretacją
Druga sprawa
Jakim cudem 2x + y = 13 w momencie w którym klasa liczy sobie 33 osoby, a
|P| −−− liczba osób uczących się portugalskiego (nie liczba osób uczących się JEDYNIE
portugalskiego)
Jeżeli zastosujesz, że |P|, |W| i |H| to liczba uczniów uczących się JEDYNIE danego języka, to
założenie, że |W| = |H| jest nadinterpretacją 


 może teraz ok?
może teraz ok?
