trójkąt michał: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku A Na boku BC obrano punkt P tak,ze |∡BPA|=2|∡BAP|

	1		1		2
Wykaż że zachodzi równość		+		=
	|BP|		|CP|		|AP|

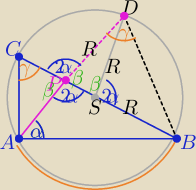Eta: Rysujemy okrąg o promieniu R opisany na tym trójkącie |BC|=2R i |SD|=R ΔDPS jest równoramienny o kątach przy podstawie 2α to |DP|=|SD|=R Trójkąty ACP i BPD są podobne z cechy (kkk) to:

	AP		CP		AP		BP
		=		i		=
	BP		PD		CP		PD

dodając stronami otrzymujemy

AP		AP		CP+BP		BC		2R
	+		=		=		=		=2
BP		CP		PD		PD		R

dzieląc stronami przez AP otrzymujemy tezę

	1		1		2
		+		=
	BP		CP		AP

==============

Mila: