Geometria analityczna rozserzona Olcix: Punkt A (2,3) jest wierzchołkiem rombu ABCD o polu równym 300 punkt S (3,4) jest środkiem symetrii tego rombu, wyznacz współrzędne pozostałych wierzchołków tego rombu

Olcix: Mam wyliczone dwie przekątne i punkt A i C d1= 10√2 d2=30√2 I C (4,11)

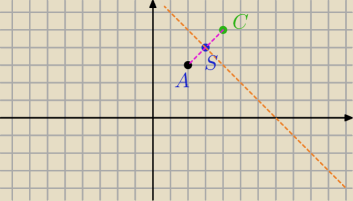
annabb: B i D daleko daleko ... B(78,−71) D (−72,79) d₁=2√2 d₂=150√2

Mila: 1 ) |AC|=2√2 √2*|BD|=300

	300
|BD|=		=150√2
	√2

1
	|BD|=75√2=|SB|
2

2) Korzystając z wektorów i przesunięcia równoległego SC^→=[1,1|, |SC|=√2 wektor SB^→⊥SC^→⇔ SB^→=k*[1,−1] =75[1,−1]=[75,−75] S=(3,4)→T_[75,−75]⇒B=(3+75, 4−75)=(78,−71) S=(3,4)→T_[−75,75]⇒D=(−72, 79) II sposób 1) równanie prostej AC i prostej BD 2) równanie okręgu : (x−3)²+(y−4)²= (75√2)² i punkt przecięcia z prostą BD