stereometria salamandra: Zadanie: https://imgur.com/a/RFuoslC Jest ok?

Mila: Jutro sprawdzę. Dobranoc

Mila: Widzę, że jest Eta, może tu spojrzy dzisiaj.

annabb: niepotrzebne to pierwsze P_P bo potem przewracasz i P_P jest całkiem inne

salamandra: Dlatego ostatecznie policzyłem inne. Na początku brakowało pomysłu i napisałem to Pp

fil: ok jest

annabb: dlatego trzeba je usunąć bo to niejednoznaczność

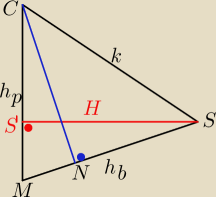
an: Można było dalej jak zacząłeś, na rysunku przekrój płaszczyzną CMS

	2
H2=k2−(		hp)2
	3

h_b²=k²−4²

	hb		3hb
hp2−(		)2=k2−(		)2
	4		4

masz h_p wyliczasz z tego prostego układu H itd.

salamandra: Jakoś sobie poradziłem z tym H, ale ciężko było wpaść na pomysł− pytanie czy objętość dobra wyszła

an: Tak

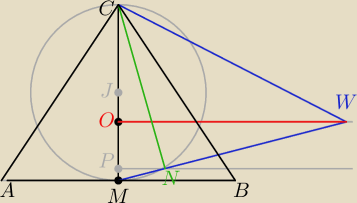
an: Czy potrafiłbyś rozwiązać takie zadanie wykreślnie. Za moich czasów "kalkulatorem" to były tablice logarytmiczne ew. suwak logarytmiczny kartka i ołówek (komputery kalkulatory to SF) takie i bardziej skomplikowane zadania sprawdzało się "szacunkowo" rysując rysunek trochę linijką trochę na "oko", na maturze nawet bez cyrkla. zamieściłem opis jak to zrobić w Geogebrze lub idąc tokiem rozumowania na na kartce może kogoś zainteresuje Wpisujesz w geogebrę

	4		1
A=(−4,0) ; B=(4,0) ; C=(0,4√3 :M=(0,0) ; O=(0,		) ; P=(0,		) J=(0,2√3)
	√3		√3

łączysz odcinkami ABC oraz CM polecasz wykreślenie obliczenie itp 1. okręgu o środku w J i promieniu CJ 2. prostych równoległych do AB (oś X), przechodzącej przez O oraz P, zaznaczasz N 3. prostej przechodzącej przez punkty MN, zaznaczasz S 4. odcinka CS= wysokość ostrosłupa

	(AB)*(CM)*(OS
5.V=		otrzymujesz V=70.75 z dokładnością do 15 po przecinku
	2*3

przeliczasz "swój pierwiastek" i widzisz, że się zgadza, nie musisz czekać, aż ktoś to przeliczy przy okazji uczysz się samoistnie wykreślania konstrukcji, widzenia przestrzennego itp. objaśnienia J środek okręgu o średnicy = wysokości podstawy O spodek wysokości, środek okręgu wpisanego w podstawę P Rzut punktu N na podstawę 1/4 OM wynika z zależności AB i DE N punkt przecięcia wysokości ściany bocznej ABS i wysokości przekroju CDE (kąt prosty oparty na średnicy okręgu J ) Dla mnie wpisanie tego zabiera trochę czasu, ale widziałem jak szybko młodzi piszą długie SMS po ciemku (dla mnie nie osiągalne) Jak Ci się to podoba.

salamandra: Na ten moment wymiękam... zbyt skomplikowane na mój poziom

an: Co tu jest skomplikowanego napisz.

salamandra: Brakuje mi chociażby treści zadania

an: Przecież to jest zadanie , do którego link zamieściłeś p/w, obudź się

an: Do Eta, Mila dlaczego moje wpisy w tym zadaniu zwłaszcza 20 maj 12:40 oraz link salamandra z treścią zostały wykasowane, zwłaszcza czy naruszyłem jakiś regulamin czy o co tu chodzi

Mila: Nie mam z tym nic wspólnego, mnie wczoraj ktoś zablokował. W połowie słowa przerwano mój wpis . Nie zaglądam do Twoich wpisów i nie wtrącam się do rozwiązań. Gdy to przeczytasz , to wykasuję mój wpis.

an: Niby jak, to Wy macie takie możliwości i prawdopodobnie macie dostęp do IP nadawców.

Mila: Nie mam dostępu do IP. Mogę tylko usunąć wpis. Dostęp do IP ma Jakub.

Mila: Ja tu widzę Twój długi wpis 12:40 z 20 maja.

Eta: @an Ja też nie mam z tym nic wspólnego, bo po zmianie komputera utraciłam możliwość moderowania Moderatorem oprócz Mili jest jeszcze ICSP

Mila: Jeszcze są inni moderatorzy, a informatycy − programiści też się mogą włamać.

salamandra: @an u mnie wszystko jest po staremu− nic nie zostało usunięte, zarówno mojego, jak i Twojego