geometria analityczna salamandra: Punkt A=(9,1) jest wierzchołkiem rombu ABCD o polu 60. Przekątna BD zawiera się w prostej l o równaniu 2x−y−7=0. Wyznacz równanie okręgu wpisanego w ten romb. 1) y=2x−7 prostopadła do niej (AC): (przekątne w rombie przecinają się pod kątem prostym) a*a1=−1

	1
a1=−
	2

A=(9,1)

	9
1=−		+b
	2

	11
b=
	2

	1		11
y=−		x+
	2		2

2) punkt przecięcia dwóch prostych (przekątnych) wyznaczy środek okręgu wpisanego.

	1		11
−		x+		=2x−7
	2		2

5		25
	x=
2		2

5x=25 x=5 S=(5,3) 3) punkt C leży na prostej AC

	1		11
C=(x,−		x+
	2		2

|AS|²=(5−9)²+(3−1)²=16+4=20 |AS|²=20 |CS|²=20 (bo przekątne w rombie się połowią, więc AS=CS)

	1		11
20=(5−x)2+(3+		x−		)2
	2		2

	1		5		25
20=25−10x+x2+		x2−		x+
	4		2		4

	25		5		25
0=5−		x+		x2+		/ *4
	2		4		4

0=20−50x+5x²+25 0=5x²−50x+45 0=x²−10x+9 Δ=64 x1=1 x2=9 <−−− współrzędne A C=(1,5) 3) B=(x,2x−7)

	e*f
P=
	2

	4√5*f
60=
	2

f=6√5 |BS|²=(5−x)²+(3−2x+7)² 45=25−10x+x²+(10−2x)² 45=25−10x+x²+100−40x+4x² x=2 v x=8 y=−3 y=9 B=(2,−3) D=(8,9) AB=√65 P=√65*h 60=√65*h

	12√65
h=
	13

	1
r=		h
	2

	180
r2=
	13

	180
(x−5)2+(y−3)2=
	13

ok?

Minato:

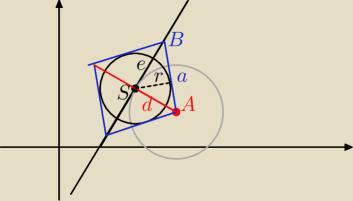an: można też tak Obliczamy d= odległość A od prostej, następnie punkt styczności okręgu o środku w A i promieniu d, z pola trójkąta prostokątnego ASB obliczamy przyprostokątną e następnie bok a rąbu i wysokość ASB na a, która jest równa promieniowi r

	2*9−1−7
d=		=√20
	√22+1

(x−9)²+(y−1)²=20 → y=2x−7 (x−9)²+(2x−7−1)²=20 ⇒x_S=5 y_S=3

	2*60
e=		=√45
	4√20

a²=e²+d²=65

	2P		2*60		180
r=		=		=√
	4a		4√65		13

	180
(x−5)2+(y−3)2=
	13

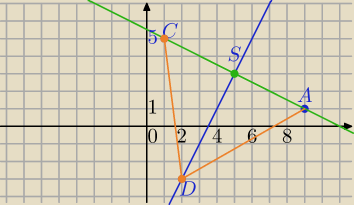Mila: Punkt A=(9,1) jest wierzchołkiem rombu ABCD o polu 60. Przekątna BD zawiera się w prostej l o równaniu 2x−y−7=0. Wyznacz równanie okręgu wpisanego w ten romb. 1) równanie drugiej przekątnej p: x+2y+C=0 i 9+2+C=0⇔C=−11

	1		11
p: x+2y−11=0 ⇔y=−		x+
	2		2

2) S− punkt przecięcia przekątnych 2x−y=7 x+2y=11 S=(5,3) 3) wsp. punktu C: AS^→=[−4,2] S=(5,3)→T_[−4,2]⇒C=(1,5) p=|AC|=2*√16+4=2*√20=4√5 4) Długość drugiej przekątnej : q 2√5*q=60

	30
q=		=6√5
	√5

5) wsp. B i D (x−5)²+(y−3)²=((3√5)² i y=2x−7 B=(8,9) , D=(2,−3) a=|AD|=√7²+4²=√65

	4*√65
5) p*r=60⇔		*r=60
	2

	30
r=
	√65

6) Równanie okręgu

	900		180
(x−5)2+(y−3)2=		⇔(x−5)2+(y−3)2=
	65		13

salamandra: dziękuję