 Wykaż, że jeżeli liczby P(A ∩ B), P(A), P(B) są odpowiednio pierwszym, drugim i trzecim wyrazem
ciągu arytmetycznego to liczba P(A ∪ B) jest czwartym wyrazem tego ciągu.
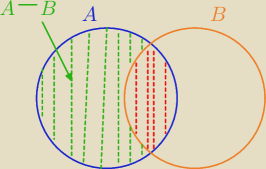
Zbiór zaznaczony czerwonymi liniami przerywanymi to zbiór A ∩ B
Skoro (P(A ∩ B), P(A), P(B)) to ciąg arytmetyczny to:
r = P(A) − P(A ∩ B) = P(A − B)
a4 = a3 + r ⇒ a4 = P(B) + P(A − B) = P(A ∪ B)
c.n.w
Jest ok ten dowód?
Wykaż, że jeżeli liczby P(A ∩ B), P(A), P(B) są odpowiednio pierwszym, drugim i trzecim wyrazem
ciągu arytmetycznego to liczba P(A ∪ B) jest czwartym wyrazem tego ciągu.
Zbiór zaznaczony czerwonymi liniami przerywanymi to zbiór A ∩ B
Skoro (P(A ∩ B), P(A), P(B)) to ciąg arytmetyczny to:
r = P(A) − P(A ∩ B) = P(A − B)
a4 = a3 + r ⇒ a4 = P(B) + P(A − B) = P(A ∪ B)
c.n.w
Jest ok ten dowód?

