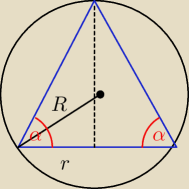
stereometria salamandra: Tworząca stożka jest nachylona do podstawy pod kątem α. Kula opisana na tym stożku ma promień R. Oblicz objętość tego stożka.

H
	=2R
sinα

2R*sinα=H

2r
	=2R
sin2α

r=R*sin2α

	1		2R3*sin22α*sinα
V=		*R2*sin22α*2R*sinα=
	3		3

jest ok? bo nie wiem czy przekrój osiowy mogę traktować tak jak bryłę w tym przypadku

fil:

l
	= 2R −−> l = 2Rsinα
sinα

	r
cosα =		−−−> r = Rsin2α
	l

	H
sinα =		−−−−> H = Rsinαsin2α
	r

	1		1
V =		* π * R2sin22αRsinαsin2α =		* π * R3 * sin32α * sinα
	3		3

Przy okazji −−− do jakiego trojkata uzywasz tw sinusow aby obliczyc H stozka?

Shizzer: Jest ok. Generalnie licząc objętość i pole powierzchni takich brył obrotowych zwykle łatwiej działać na samych przekrojach, bo w przekrojach osiowych masz wszystkie dane potrzebne do rozwiązania. Mi się szkicowanie całych brył łącznie z podstawami przydało jak w stożek musiałem wpisywać sześcian albo prostopadłościan np. − wtedy się to przydaje. Jeśli nie wiem jak wygląda przekrój osiowy danej bryły obrotowej wpisanej w inną bryłę to szkicuję całość i tyle

salamandra: Racja @fil, trochę się pospieszyłem z wysokością

Shizzer: No i starając się pomóc sam popełniłem ten błąd

salamandra:

	H
@fil, sinα=		, więc H=2R*sin2α chyba
	l

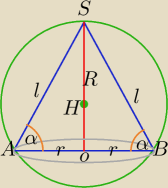
Mila: Dane : α, R 1)|OS|=H W ΔABS: Z tw. sinusów:

l
	=2R⇔ l=2R sin α
sinα

2r
	=2R⇔r=R sin(2α)
sin(180−2α

2) W ΔAOS:

	H
sinα=		⇔H=lsinα⇔H=2R sin2α
	l

	1
3) V=		π*(R sin(2α) )2*2Rsin2(α)
	3

	1
V=		πR3*sin2α*sin2(2α)
	3

========================

salamandra: tyle i mi wyszło po korekcie, dzięki za potwierdzenie