planimetria
fil: Na bokach AB, BC i CA trójkata ABC wybrano odpowiednio punkty D, E i F. Wykaz,˙ ze˙
okregi opisane na trójkatach ADF, BED i CFE przecinaja sie w jednym punkcie.
17 maj 13:22
Minato: Na discordzie ostatnio to pokazywałem, poszukaj tam
17 maj 13:27
fil: Tam sporo przewijania

, spytalem bo mi nawet na moim rysunku pomocniczym te okregi sie
przecinaja w roznych miejscach
17 maj 13:38
17 maj 14:03
Minato:
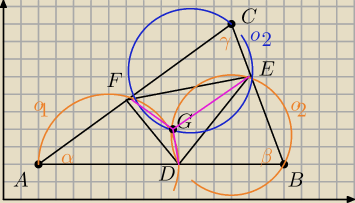
NIech O
1 i O
2 przecinają się w punkcie G.
Pokażemy, że czworokąt GFCE jest wpisany w okrąg O
3.
Czworokąt ADGF jest wpisany w okrąg O
1, zatem ∡FGD = 180−α
Czworokąt GDBF jest wpisany w okrąg O
2, zatem ∡DGE = 180−β
∡FGE = 360 − (180−α+180−β) = α+β
Suma miar kątów w trójkącie ABC wynosi 180 = α+β+γ ⇒α+β = 180−γ = ∡FGE
WNIOSEK: Czworokąt GFCE jest wpisany w okrąg 0
2, zatem Δ CFE jest opisany na 0
2,
stąd G jest punktem przecięcia się okręgów O
1, O
2, O
3.
17 maj 14:11
Minato:
Fran123 zasada panująca na forum: pomagasz albo odsyłasz do zasobów tego forum.
Nie reklamuj innych

17 maj 14:12
Minato:
Poprawka niebieskie okrąg, to o
3, wiec trzeba zmodernizować rozwiązanie

WNIOSEK: Czworokąt GFCE jest wpisany w okrąg
O3, zatem Δ CFE jest opisany na
O3,
stąd G jest punktem przecięcia się okręgów O1, O2, O3.
17 maj 14:15
17 maj 15:06
fil: dziekii, wlasnie czegos z takimi dowodami szukalem
17 maj 15:24
 , spytalem bo mi nawet na moim rysunku pomocniczym te okregi sie
przecinaja w roznych miejscach
, spytalem bo mi nawet na moim rysunku pomocniczym te okregi sie
przecinaja w roznych miejscach
 NIech O1 i O2 przecinają się w punkcie G.
Pokażemy, że czworokąt GFCE jest wpisany w okrąg O3.
Czworokąt ADGF jest wpisany w okrąg O1, zatem ∡FGD = 180−α
Czworokąt GDBF jest wpisany w okrąg O2, zatem ∡DGE = 180−β
∡FGE = 360 − (180−α+180−β) = α+β
Suma miar kątów w trójkącie ABC wynosi 180 = α+β+γ ⇒α+β = 180−γ = ∡FGE
WNIOSEK: Czworokąt GFCE jest wpisany w okrąg 02, zatem Δ CFE jest opisany na 02,
stąd G jest punktem przecięcia się okręgów O1, O2, O3.
NIech O1 i O2 przecinają się w punkcie G.
Pokażemy, że czworokąt GFCE jest wpisany w okrąg O3.
Czworokąt ADGF jest wpisany w okrąg O1, zatem ∡FGD = 180−α
Czworokąt GDBF jest wpisany w okrąg O2, zatem ∡DGE = 180−β
∡FGE = 360 − (180−α+180−β) = α+β
Suma miar kątów w trójkącie ABC wynosi 180 = α+β+γ ⇒α+β = 180−γ = ∡FGE
WNIOSEK: Czworokąt GFCE jest wpisany w okrąg 02, zatem Δ CFE jest opisany na 02,
stąd G jest punktem przecięcia się okręgów O1, O2, O3.

 WNIOSEK: Czworokąt GFCE jest wpisany w okrąg O3, zatem Δ CFE jest opisany na O3,
stąd G jest punktem przecięcia się okręgów O1, O2, O3.
WNIOSEK: Czworokąt GFCE jest wpisany w okrąg O3, zatem Δ CFE jest opisany na O3,
stąd G jest punktem przecięcia się okręgów O1, O2, O3.