zbiory
salamandra:
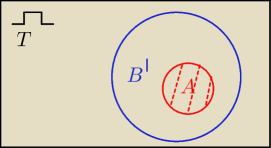
Niepuste zdarzenia losowe A i B zawarte w Ω sa takie, że A ⊆ B', gdzie B' oznacza zdarzenie
przeciwne do zdarzenia B. Wynika stąd, że
A) P(A|B)<P(B|A)
B) P(A|B) + P(B|A)=1
C)P(A|B)=P(B|A)
D) P(A|B)>P(B|A)
Tak te zbiory wyglądają?
17 maj 12:51
salamandra: to "T" przypadkowo
17 maj 12:51
fil:
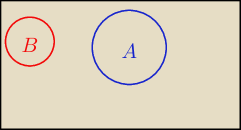
17 maj 13:01
Bleee:
@salamandra −−−− A ⊆ B' oznacza że AnB = ∅ czyli P(AnB) = 0
17 maj 13:07
salamandra: Tak, wiem, ale narysowałem z B’ bo nie byłem pewien czy B zawiera się w A czy A zawiera się w B
17 maj 13:07
salamandra: Obstawiam odpowiedz C

17 maj 13:13
fil: tak, bo P(AnB) = 0
17 maj 13:14
Adamm:
Mogą być niepuste, a prawdopodobieństwo mieć zerowe
17 maj 13:17
salamandra: Nie bardzo rozumiem Adamm?
17 maj 13:19
ABC:
W szkole średniej tak nie będzie jak on mówi ,wy macie dyskretny rachunek pstwa
17 maj 13:22
 Niepuste zdarzenia losowe A i B zawarte w Ω sa takie, że A ⊆ B', gdzie B' oznacza zdarzenie
przeciwne do zdarzenia B. Wynika stąd, że
A) P(A|B)<P(B|A)
B) P(A|B) + P(B|A)=1
C)P(A|B)=P(B|A)
D) P(A|B)>P(B|A)
Tak te zbiory wyglądają?
Niepuste zdarzenia losowe A i B zawarte w Ω sa takie, że A ⊆ B', gdzie B' oznacza zdarzenie
przeciwne do zdarzenia B. Wynika stąd, że
A) P(A|B)<P(B|A)
B) P(A|B) + P(B|A)=1
C)P(A|B)=P(B|A)
D) P(A|B)>P(B|A)
Tak te zbiory wyglądają?

