dowód Fran123:

	1
a) Wyznacz a,b takie że |ax+b−√x| ≤		dla 1 ≤ x ≤ 4.
	24

	1
b)Wykaż że stałą		nie może być zastąpiona mniejszą liczbą.
	24

PW: 1 ≤ x ≤ 4 1 ≤ √x ≤ 2 (1) − 2 ≤ − √x ≤ −1 Dla a > 0 (2) a ≤ ax ≤ 4a A (1) i (2) a + b − 2 ≤ ax + b − √x ≤ 4a + b − 1 Narzucony warunek oznacza, że musi być jednocześnie

	1		1
a + b − 2 ≥ −		i 4a + b − 1 ≤
	24		24

	47		25
− (a + b) ≤		i 4a + b ≤
	24		24

Po dodaniu stronami 3a ≤ 3 a ≤ 1 No i brakuje w treści zadania założeń dla liczb a i b, albo nie mam dalej pomysłu.

Fran123: a, b rzczywiste

fil:

	1
Mozna wyjsc od czegos takiego: √(ax + b − √x)2 <=
	24

Fran123: No fil mozna ale co z tym?

PW: Na razie widzę u siebie pomyłkę w piątym wierszu od dołu − powinno być

	47
− (a + b) ≤ −		.
	24

Wtedy dodanie stronami daje

	22
3a ≤ −		,
	24

a to daje sprzeczność z założeniem, że a > 0. Może to trzeba pociągnąć.

Minato: albo podstawić √x = t dla t∊[1, 2] i zbadać zbiór wartości funkcji f(t) = |at²−t+b| ja bym poszedł w tę stronę

Fran123: A jak dalej z tym?

ABC: a gdyby przeskalować aproksymację jednostajną pierwiastka na przedziale [0,1] ? https://commons.wikimedia.org/wiki/File:Sqrt_uniform_approximation.svg

Fran123: To zadanie z poziomu liceum....

ABC: dzisiejszego liceum? to naprawdę wyzwanie, ja w swoim liceum miałem szereg Taylora

ABC: chyba że pójdzie z pierwszej pochodnej samej , może i tak

Iks: Nie ma w liceum szeregu Taylor

ABC: rozwaliłem to z pierwszej pochodnej , ale musiałem skorzystać z twierdzenia Kołmogorowa , żeby

	1
wypisać układ 4 równań z 4 niewiadomymi, faktycznie wychodzi		, ale jak to zrobić
	24

prościej?

ABC:

	1		17
szukana prosta to y=		x+		, jeśli ktoś spróbuje prościej żeby znał wynik
	3		24

Iks: A jakie to twierdzenie kolmogirowa

PW: O 15:42 doszliśmy do wniosku, że nie może być a > 0. Wobec tego − dla a < 0 − nierówność (2) ma postać a ≥ ax ≥ 4a (2') − a ≤ − ax ≤ − 4a, co po dodaniu stronami z nierównością (3) 1 ≤ √x ≤ 2 daje − a + 1 ≤ − ax + √x ≤ − 4a + 2. − a − b + 1 ≤ − ax − b + √x ≤ − 4a − b + 2. Narzucony w treści zadania warunek oznacza, że

	1		1
−		≤ − a − b + 1 i − 4a − b + 2 ≤
	24		24

	1		1
a + b − 1 ≤		i − 4a − b + 2 ≤
	24		24

	25		47
a + b ≤		i − 4a − b ≤ −
	24		24

Po dodaniu stronami

	22
− 3a ≤ −
	24

	22
3 a ≥
	24

Znów otrzymaliśmy sprzeczność − zakładaliśmy a < 0 . Wniosek − należy sprawdzić dla a = 0. Badana nierówność ma postać

	1
|b − √x| ≤
	24

	1		1
−		≤ b − √x ≤		,
	24		24

po dodaniu stronami nierówności (3) otrzymamy

	1		1
1 −		≤ b ≤ 2 +
	24		24

Wygląda na to, że

	1		1
a = 0 i b − pewna liczba z przedziału <1 −		, 2 +		>
	24		24

Skoro to zadanie na poziomie liceum, to zadający pytanie licealista na pewno sobie poradzi z dokończeniem.

ABC: jak ci napiszę to twierdzenie w języku analizy funkcjonalnej to i tak nic nie zrozumiesz, ono mówi coś takiego niech f(x)=√x g(x)=ax+b żeby znaleźć a, b trzeba rozwiązać układ 4 równań : f(1)−g(1)=−δ f(4)−g(4)=−δ f(c)−g(c)=δ f'(c)−g')c)=0 gdzie c∊(1,4) pewien punkt a δ−maksymalny błąd wychodzi z tego a=1/3 b=17/24 c=9/4 δ=1/24

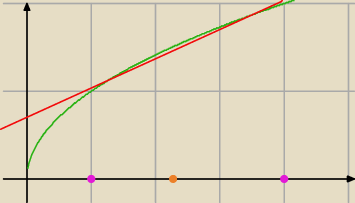
ABC: tak to wygląda

PW: Bez bicia sie przyznaję − musiałem gdzieś się pomylić. Trzeba było zacząć od rysunku ax+b i √x.

PW: O, zanim pomyślałem, to rysunek się pojawił

ABC: dziś proza życia zmusza mnie do oderwania się od tego i rozpoczęcia sprawdzania testów w nauczaniu zdalnym , ale może ktoś to elementarnie uzasadni

PW: Już wiem na czym polegał mój błąd logiczny, w ten sposób nie da się tego pokazać. Uczniowskie podejście może być takie: 1. Rysujemy na początek prostą przechodzącą przez punkty (1, 1) i (4, 2). Jest to najprostsza "przymiarka" − a nuż taka prosta spełni warunki zadania? Prosta ma równanie

	1		2
(1) y =		x +		.
	3		3

2. Sprawdzamy jakie jest maksimum różnicy

	1		2
(2) f(x) = √x − (		x +		)
	3		3

	9
na zadanym przedziale. Okazuje się, że maksimum jest osiągnięte w punkcie x0 =		i jest
	4

	2
ono równe		(badamy różnicę za pomocą pochodnej)..
	24

	1
3. Wystarczy więc wykres funkcji (1) przesunąć w górę o		− na obydwu krańcach
	24

	1		1
przedziału <1, 4> różnica (2) wyniesie −		, a w punkcie x1 będzie równa		, zaś
	24		24

w pozostałych punktach przedziału będzie mniejsza. Tu wypadałoby zrobić drugi rysunek pokazujący funkcję liniową po przesunięciu. Jest ona określona wzorem

	1		2
y =		x +		+ U{1}{24
	3		3

	1		17
y =		x +		.
	3		24

Zgadza się, profesorze ABC. Trzeba jednak powiedzieć, że jak na liceum, to dość nietypowe zadanie, z serii − A jak ja niby miałbym na to wpaść? Druga część zadania też nie jest oczywista. Wymaga pomyślenia:

	1
− A co by było, gdyby wziąć prostą nachyloną pod innym kątem α, takim że a2 = tgα ≠		?
	3

i pokazania, że wtedy znajdzie się punkt x₂ w przedziale <1, 4>, dla którego

	1
|a2x2 + b − √x2| >
	24

(przy każdym b).