rówananie yep: Wyznacz wszystkie a że x³ − x + a = 0 ma trzy różne rozwiązania będące liczbami całkowitymi.

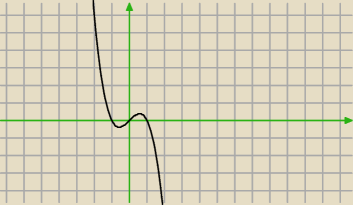
a7: x(1−x²)=a a=0 x₁=0 x₂=1 x₃=−1

yep: Teraz mam sprawdzać dla a=1, 2,3....−1,−2...

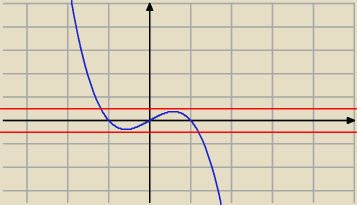ABC: nie zrozumialeś rysunku zauważ że równanie x³−x+a=0 możemy przekształcić do postaci a=x−x³ i z wykresu widać , że ono ma trzy rozwiązania rzeczywiste w tak wąskim zakresie zmienności a , że jedyną liczbą całkowitą do sprawdzenia jest 0 (a musi być całkowite, ze wzorów Viete'a to wynika)