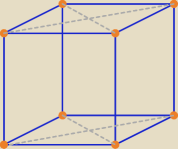
Prawdopodobieństwo + stereometria Shizzer: Spośród wierzchołków sześcianu wybieramy losowo cztery. Oblicz prawdopodobieństwo tego, że nie istnieje prostokąt, którego wierzchołkami są wylosowane punkty. Ω − zbiór zdarzeń, w których jednocześnie zostały wylosowane 4 dowolne wierzchołki sześcianu

	8 4
|Ω| =		= 70

A − zbiór zdarzeń, w których 4 wylosowane wierzchołki nie tworzą prostokąta Zatem A' − zbiór zdarzeń, w których 4 wylosowane wierzchołki tworzą prostokąt |A'| = 6 + 2 = 8 Ta wyliczona moc zbioru A' jest nieprawidłowa niestety. 6 prostokątów zostanie utworzonych po wylosowaniu 4 wierzchołków każdej ze ścian sześcianu. 2 prostokąty powstaną jeśli zostaną wylosowane 4 wierzchołki zawierające końce którejś z przekątnych podstaw sześcianu. Prawidłowa moc zbioru zdarzeń A' jest taka: |A'| = 6 + 6 = 12 Ktoś mógłby mi pomóc odnaleźć pozostałe prostokąty?

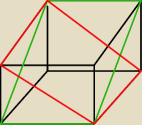
ICSP: te uwzględniłeś ? 2 zielone (drugi zaczynający się od górnej krawędzi i idący do dolnej) 2 czerwone 6 ścian sześcianu 2 tak jakby pionowe o boku będącym przekątną podstawy i drugim boku równym wysokości

Minato: 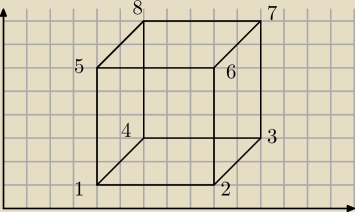ICSP super Jak na to wpaść? Z wierzchołka 1 możesz poprowadzić 7, i zobacz kiedy mogą powstać prostokąty.

Shizzer: 2 pionowe uwzględniłem natomiast nie uwzględniłem tych, które zawierają przekątne ścian przeciwległych. Dziękuję bardzo za pomoc! Teraz już wszystko widzę

Shizzer: Dokończę zadanie może komuś się przyda. Ω − zbiór zdarzeń, w których jednocześnie zostały wylosowane 4 dowolne wierzchołki sześcianu A − zbiór zdarzeń, w których 4 jednocześnie wylosowane wierzchołki nie tworzą prostokąta A' − zbiór zdarzeń, w których 4 jednocześnie wylosowane wierzchołki tworzą prostokąt

	8 4
|Ω| =		= 70

|A'| = 6 + 6 = 12 (6 prostokątów ze ścian sześcianu, 2 z przekątnych podstaw i 4 z przekątnych ścian przeciwległych)

	12		6
P(A') =		=
	70		35

	29
P(A) = 1 − P(A') =
	35