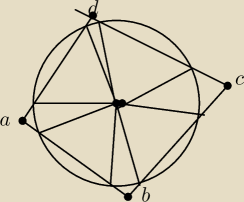
Okrąg jul1a: Okrąg przecina wszystkie cztery boki czworokąta, z każdego z nich wycina cięciwe tej samej długości. Pokaż, że w ten czworokąt da się wpisać okrąg. Żeby w czworokąt wpisać okrąg trzeba udowodnić, że suma przeciwległych boków jest sobie równa. Próbowałam wykazać to z twierdzenia o siecznych jednak to nic nie daje. Ma ktoś pomysł jak tego dowieść?

fil: Zauwaz, ze te cztery trojkaty sa rownoramienne, narysuj ich wysokosci i wyciagnij wniosek

jul1a: Tak, to wcześniej zauważyłam, że są przystające równoramienne. Jednak po narysowaniu ich wysokości nie widzę zależności z bokami tego czworokąta

fil: A po co, zobacz na ich wysokosci i czym sa

jul1a: Są równoległe do boków czyli mają taką samą długość?

fil: Wysokosci − wychodza z tego samego punktu, sa takiej samej dlugosci (trojkaty przystajace) i padaja na bok pod katem prostym, czyli.....

jul1a: dzielą boki na połowy? chyba jest coś ze mną nie tak, bo nadal tego nie widzę...

fil: To znaczy, ze okrag w punkcie P jest styczny do wszystkich bokow −−− czyli mozna w ABCD wpisac okrag

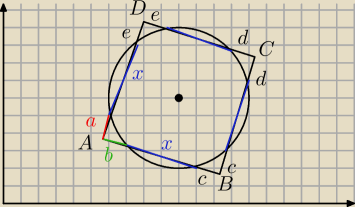
Minato: Z tw. o siecznych mamy a(a+x)=b(b+x) a²−b²+ax−bx=0 (a−b)(a+b)+x(a−b)=0 (a−b)(a+b+x)=0 a=b Analogicznie dla kolejnych odcinków. AB+DC = 2x+a+c+d+e BC+AD = 2x+a+c+d+e, zatem AB+DC = BC+AD, stąd w czworokąt ABCD można wpisać okrąg

jul1a: Dziękuje