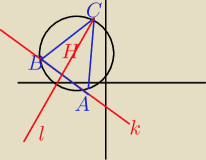
geometria mr t: W okrąg dany równaniem: x²+y²+4x−4y−1=0 wpisano trójkąt równoramienny. Podstawa tego trójkąta zawiera się w prostej o równaniu k: y=−x−3. Oblicz pole trójkąta. l: y=x+4 (proste l i k przecinają się pod kontem prostym) A(−2;−1) B(−5;2) C(0;4) |AB|=3√2

	7√2
H=
	2

P_t=10,5

	9+9√2		9√2−9
Jednak w odpowiedziach mam, że pole wynosi		lub
	2		2

Pytanie czy to błąd w odpowiedziach czy ja coś źle zrobiłem?

Bleee: Punkt C=(0, 4) nie należy do okręgu

Bleee: Druga sprawa − nie rozpatrzyles przypadku że C leży poniżej prostej k (patrz swój rysunek)

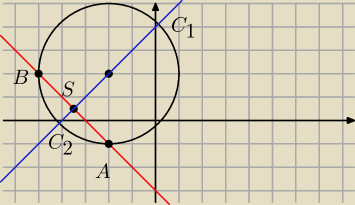Minato: x²+y²+4x−4y−1=0 (x+2)²+(y−2)²=9 S(−2, 2), r=3 A = (−2, −1) B = (−5, 2)

	−2+(−5)		−1+2		−7		1
Środek odcinak AB ma współrzędne S = (		,		) = (		,		)
	2		2		2		2

Prosta prostopadła do k i przechodząca przez punkt S y = x+b

1		7
	= −		+b ⇒ b=4 ⇒ y=x+4
2		2

Punkt przecięcia się prostej y = x+4 oraz okręgu (x+2)²+(y−2)²=9 (x+2)² + (x+2)² = 9

	9
(x+2)2=
	2

	3√2		3√2
x+2 =		lub x+2 = −
	2		2

	3√2−4		−3√2−4
x =		lub x =
	2		2

dokończ

mr t: fakt... dzieki

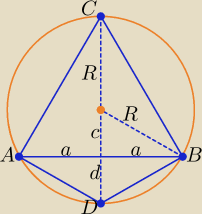Bogdan: Jeśli dane są: a, R to: c = √ R² − a² i d = R − c Pola trójkątów: P_ABC = a*(R + c), P_ABD = a*d.

	3
W tym zadaniu: a =		√2, R = 3
	2