dowod fil: Na bokach AB , AD i BC rombu ABCD wybrano odpowiednio punkty K,L i M w ten sposób, że odcinki KL i KM są równoległe do przekątnych rombu. Wykaż, że odcinek LM przechodzi przez punkt przecięcia przekątnych rombu.

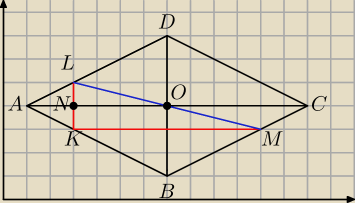
Minato: ΔLNO ~ ΔLMK (bkb) przy czym LO i LM leża na jednej prostej ⇒ LM przechodzi przez punkt przecięcia się przekątnych rombu

fil: a nie skorzystales przy tym dowodzie z tezy?

fil: Bo my nie wiemy czy przechodzi, a zalozyles ze przechodzi, rownie dobrze moze byc trojkat LNP podobny do LMK, gdzie P lezy na odcinku NO i P != O

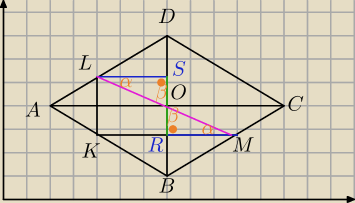
Minato: Słusznie, to inaczej Niech S i R będą rzutami prostokątnymi punktów L oraz M na prostą BD. ΔLSO i ΔMRO mają wspólny wierzchołek O, boki SO i OR leża na jedne prostej, OS = OR oraz SL = RM oraz ∡MRO = ∡LSO=90, zatem te trójkąty są przystające, wobec czego mają kąty tej samej miary, stąd mamy, że prosta MO i OL są nachylone pod tym samym kątem do prostej AC. co więcej obydwie przechodzą przez punkt O, zatem są tą samą prostą. Wobec czego LM przechodzi przez O

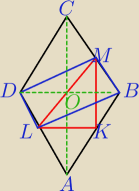
fil: Moze byc tak DLBM jest rownoleglobokiem, a czyli jego przekatne LM i DB dziela sie w polowe, czyli z tego wynika, ze LM przechodzi przez srodek odcinka DB (punkt przeciecia sie przekatnych w rombie)

fil: oczywiscie |LB| = |DM|