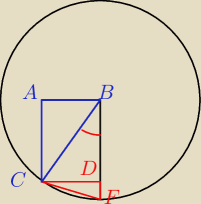
Planimetria Poprostupatryk: Czy ΔABC ~ ΔCDF? Jeżeli tak to jak to udowodnić?

a7: a czy kąt ACB = kąt DCF ?

a7: czy kąt BCF jest prosty?

Poprostupatryk: No właśnie tego nie wiem. Gdybym wiedział, że DCF = ACB to byłby podobne. Za mało danych jest według Ciebie? Konstruuję pewną część i chcę obliczyć odległość AB, dla której punkt C znajdzie się w F po obróceniu boku AC o kąt jakiś tam od osi obrotu w punkcie B

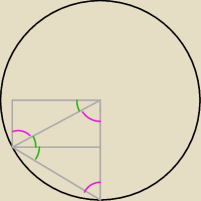
a7: np. tutaj są podobne, a nawet przystające

a7: no to chyba chodzi Ci o przesunięcie boku BC o kąt 60^o?, bo nie rozumiem jakie przesunięcie boku AC?

Poprostupatryk: Czyli dopiero dla określonego kąta różowego, te trójkąty są przystające?

a7: AB o kąt 60^o?

a7: tzn. różowy to chyba 60^o

Poprostupatryk: W mojej konstrukcji planuję raczej ~15^o, chciałbym jakoś zbudować równanie które będzie działać nie tylko dla określonego kąta Czekaj spróbuję, jakoś narysować jeszcze

a7: kąt BCF nie może być prosty, gdyż BF bylby przeciwprostokątną a BF=BC anie większe

a7: także z Twojego pierwotnego rysunku nie są to trójkąty podobne

a7: na rysunku 00:37 różowy to 60 a zielone to 30

a7: dobra czekam

Poprostupatryk: No rozumiem. Mam pewną teorię https://zapodaj.net/images/43c08d3deb5ac.jpg

a7: odległość AB=r√3/2 (mamy trójkąt ekierkę)

a7: (to znaczy odpowiednik AB, ale na drugim rysunku)

a7: może jeśli to cześć materialna, a kąt odpowiednio mały to nie musi być to podobieństwo "w pełni" precyzyjne, a część będzie działać prawidłowo. Na gruncie teorii na razie wychodzi chyba tak jak mówię

Poprostupatryk: Pamiętam z fizyki pewną zależność z wahadła matematycznego. Wzory na nie działają gdy kąt (u mnie na rysunku) θ jest mały, tzn mniejszy od 10^o. Bo sinθ ~ θ.

	x		x
To z mojego rysunku: sinθ=		, więc θ=
	R		R

Ja w projekcie mam określone a i b i chciałbym znaleźć maksymalną odległość x dla której bok BA mi zapierniczy w punkt A^' i się zatrzyma na przeszkodzie Kurde nie wiem czy teraz bzdury gadam jakieś, bo późno jest

a7: gdyby kąt BCF był prosty ( a jest to niemożliwe jak już uzasadniłam) to byłyby podobne

a7: nie , nie bzdury, chyba kumam

a7: a masz możliwość testowania, czy to droga część?

Poprostupatryk: Chciałbym właśnie zbudować równanie na x, zależne od a, b i θ

a7: najlepiej prawie od razu testować

Poprostupatryk: Na testy sobie nie mogę pozwolić bo tej części fizycznie nie mam, chcę właśnie ją zaprojektować do druku 3D

a7: dobra a jak duża ta część i jak duża przeszkoda, czy przeszkodę da się powiększyć żeby skorygować co trzeba

a7: to lepiej, żeby jeszcze się ktoś wypowiedział, ale zaraz może jeszcze dorzucę jakieś trzy grosze, moment

Poprostupatryk: Raczej małe są te części, planuję żeby a = 5cm a b było w granicy 2mm

a7: a przeszkoda?

Poprostupatryk: No dobra, to dzięki za poświęcenie ja pokombinuję jeszcze i może przetestuję to w jakimś programie

Poprostupatryk: przeszkoda będzie taka długa jak na rysunku raczej, a odległość w pionie od BA wynosi b właśnie czyli ~2mm

a7: ale nie rozumiem co ma o co się zatrzymać?

a7: to znaczy masz na myśli AB z rysunku odręcznego, a nie z 00:21, (niekonsekwencja w oznaczeniach mnie zmyliła)

Poprostupatryk: No patrz, wyobraźmy sobie że odcinek BA to cienka linijka która jest zaczepiona do sztywnego pręta x. O to oś obrotu. Jak puścimy tą linijkę to zatoczy ona łuk taki jak narysowany na moim zdjęciu. Gdy x będziemy zmniejszać, to znaczy, OŚ obrotu O będziemy przybliżać do linijki AB to ten tor będzie inny, promień wodzący (chyba tak to się nazywa) będzie mniejszy

Poprostupatryk: No tak, rysunek odręczny chyba lepiej to odwzorowywuje

a7: no tak, ale AO=R, więc niezależnie od x linijka Ci się zaczepi, bo właśnie AO=R, chyba nie łapię

a7: PS. zrobiłam model z tekturki i kartki i może to metoda też dla Ciebie, (niezależnie od tego, że nie łapię, to wydaje mi się, ze to łatwy, szybki i dobry sposób na "prototyp prototypu")

Poprostupatryk: No tak zaczepi się, bo ten przypadek narysowałem jaki graniczny, dla mniejszej wartości x nie zaczepi się. (x licząc od AB, dosłownie mówiąc, jak środek okręgu przesunie się w lewo, zmieni się również promień, bo odległość AO będzie inna) Chodźmy spać, może jutro ktoś się wypowie jeszcze XD

Poprostupatryk: No myślę, że podobną metodą będę kombinował w programie ten model, budowanie tych równań to chyba trochę overkill, ale fajnie było użyć trochę głowy

a7: ja jeszcze trochę posiedzę, ale dobrego snu, jutro może przyjdą nowe pomysły i może Ktoś coś ciekawego powie...

a7: (jutro w sensie dzisiaj )

Poprostupatryk: Mam teorię YAY https://www.desmos.com/calculator/edv5szc3kr- wykres Niech A=(0,a+b) B=(0,b) O=(x_o,a+b) |AO|=x_o |BO|=R C=(x_o,0) – punkt styku z przeszkodą D=(x_o),b) |AB|=a |BO|=x_o |AO|=R kąt BAO = θ okrąg o: (x−x_o)²+[y−(a+b)]²=R² B należy do okręgu o: x_o²+[b−(a+b)]²=R² x_o²+a²=R² 1^o − wyszedł normalny Pitagoras

	xo
tgθ =		oraz 1o:
	a

	xo2		R2*tg2θ
xo2+		=R2 ⇒ xo2=		2o
	tgθ		tg2θ+1

R=a+b oraz 2^o:

	(a+b)2*tg2θ
xo2=
	tg2θ+1

Znalazłem długość x_o, dla której jak obrócę bryłę sztywną o długości a o kąt θ, to ona uderzy w przeszkodę odległą o b licząc pionowo od punktu B. Więc muszę wybrać takie x<x_o dla danego kąta θ. Nie wiem czy to jest merytorycznie poprawne. Wyprowadziłem równanie, które zawiera tylko te dane które są stałe. Wieczorem może będę miał czas żeby przetestować to w praktyce

Poprostupatryk: Wykres tu: https://www.desmos.com/calculator/f7qkutowos