Topologia WhiskeyTaster: Mamy przestrzeń metryczną (X, d_X) i niech Y ⊂ X. Wtedy obcięcie d_Y = d_X | Y² metryki d_X do Y jest metryką generującą w Y topologię T(d_Y), której elementy są śladami zbiorów otwartych w (X, d_X) na Y, tzn. T(d_Y) = {U ∩ Y: U ∊ T(d_X)} Trochę tego nie rozumiem. Weźmy (R², d_e) i Y = [0, 1]². Biorąc B( (0,0), 1) ∊ T(d_X) to widzimy z tej definicji mamy, że (B( (0,0), 1) ∩ Y) ∊ T(d_Y). Ale w (0, 0) ∊ Y nie można przecież opisać kuli. Czyli źle myślę, gdy czytam, że T(d_Y) to zbiór wszystkich przekrojów elementów topologii T(d_X) ze zbiorem Y?

ABC: nie za bardzo rozumiem o co ci chodzi , przecież te nowe kule nie muszą być kulami sensu stricto

WhiskeyTaster: Dlaczego? Metryka na podzbiorze pozostaje taka sama, prawda? Więc kule też powinny zachować swój kształt. A tu na przykład dostajemy, że kulą jest zbiór, który nie będzie ani otwarty, ani domknięty.

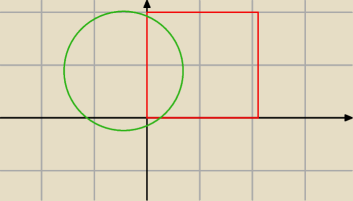
ABC: ja cię zrozumiałem tak ,że masz problem z tym że cześć wspólna zielonego z czerwonym jest kulą

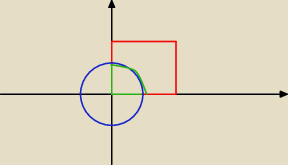
WhiskeyTaster: Trochę brzydko, no ale widać o co mi chodzi. Wydawało mi się, że te ślady zbiorów też powinny być zbiorami otwartymi z metryką d_Y, która jest metryką d_X z obcięciem do Y.

WhiskeyTaster: ABC, bo właśnie o to mi chodzi Myślałem, że skoro d_Y jest metryką d_X obciętą do Y, to powinniśmy móc dla każdego punktu promień tak, by kula o tym środku i promieniu zawierała się w tym zbiorze.

ABC: no i znajdziesz dla każdego punktu tak

WhiskeyTaster: Nawet dla punktów brzegowych?

	1
Przecież biorąc B((0,		), r) na tym kwadracie, to taka kula w metryce euklidesowej nie
	2

zawiera się w tym zbiorze dla dowolnego r. Mógłbyś rozjaśnić? Jakoś z tym mam problem

ABC: ty masz problem z definicją kuli otwartej w danej przestrzeni jak widzę po obcięciu wszystko co było na zewnątrz przestaje dla ciebie istnieć

WhiskeyTaster: Ach, więc tu tkwi mi problem. Innymi słowy mamy pustą przestrzeń poza zbiorem, do którego obcięliśmy, a więc nie ma tam żadnych elementów. I w takim razie faktycznie, kula będzie otwarta i będzie zawarta w tymże obcięciu

ABC: poczekaj, od północy mam darmowy transfer, wrzucę ci fajną książkę na jakiś upload której pierwsze wydanie uratowało mi dupę gdy sam byłem studentem

WhiskeyTaster: Dobrze, dziękuję Ogółem korzystam ze skryptu, ale czasem są rzeczy po łebkach, jak to tutaj. Nie myślałem tak o obcięciu, jak powinienem.

ABC: https://megawrzuta.pl/download/7a1ff220908684b091beb64364360d99.html

WhiskeyTaster: Fajnie, dziękuję. Widzę, że jest sporo zadań To jest przewaga książek nad skryptami

ABC: i co najważniejsze porządne rozwiązania na których różnych technik można się nauczyć

WhiskeyTaster: Fajnie, jeszcze raz dziękuję, na pewno się przyda − nie tylko teraz