Trudniejsza geometria Heniu: Przekątne AC i BD czworokąta wypukłego ABCD przecinają się w punkcie P . Punkt M jest środkiem boku AB . Prosta MP przecina bok CD w punkcie Q . Dowieść, że stosunek pól trójkątów BCP i ADP jest równy stosunkowi długości odcinków CQ i DQ

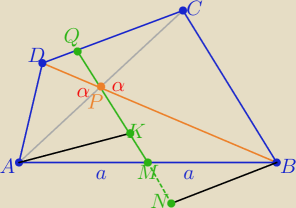
Eta: Jeden ze sposobów: 1/prowadzimy odcinek AK ∥DC i odcinek BN∥DC to z tw. Talesa:

	AK		AM
		=		= 1 bo M jest środkiem AB ⇒ AM=MB, to AK=BN
	BN		MB

zatem

P(BCP)		CP*BP*sinα		CQ*BN
	=		=		i AK=BN
P(ADP)		AP*DP*sinα		AK*DQ

to

	P(BCP)		CQ
		=
	P(ADP)		DQ

============= c.n.w

Heniu: Dziękuję

jas:

	CP*BP		CQ*BN
Pytanko skąd się wzięło przejście na		=		bo nie widzę tego ?
	AP*DP		AK*DQ