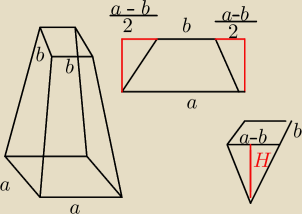
Przedstawiona na rysunku bryła to ostrosłup prawidłowy czworokątny ścięty płaszczyzną
równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa H,a a i b (a > b ) są
długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
V ostrosłupa stworzonego z "doklejenia", co w rezultacie tworzy nam graniastosłup:
| 1 | 1 | abH−b2*H | bH(a−b) | |||||
V= | (a−b)b*H= | (ab−b2)*H= | = | |||||
| 3 | 3 | 3 | 3 |
| bH(a−b) | ||
V ostrosłupa ściętego=a2*H− | ||
| 3 |
| H | ||
V= | (a2+b2+ab) | |
| 3 |
właśnie miałam pisać.
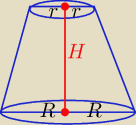Jeszcze wzór na objętość stożka ściętego
| π H | ||
V= | (R2+rR+r2) | |
| 3 |
wskazać błąd? bo musiałem jakoś sobie radzić bez znajomości gotowego
wzoru 
dobrej nocy!
Może ktoś inny się pokusi, bo myślałem, że w dobrą stronę idę, a tu klapa najprawdopodobniej
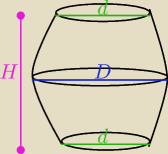Może się w przyszłości przydać :
Wzór na objętość beczki ( na bimber dla teścia)
| πH | ||
V= | (2D2+d2) D, d −− długości średnic | |
| 12 |
| H(a2 + ab + b2 | ||
V = | ||
| 3 |
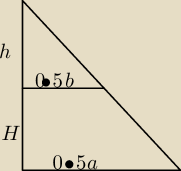
| 2h | 2(h + H) | ||
= | |||
| b | a |
| bH | ||
h = | ||
| a − b |
| b2 | bH | Hb3 | ||||
Vscietego = | * | = | ||||
| 3 | a − b | 3(a − b) |
| a2 | a2 | aH | a3H | |||||
Vcalego (ze scietym) = | * (H + h) = | * | = | |||||
| 3 | 3 | a − b | a − b |
| a3H − b3H | ||
Vpozostale = Vcalego (ze scietym) − Vscietego = | = | |
| 3(a − b) |
| H(a − b)(a2 + ab + b2) | H(a2 + ab + b2) | |||
= | = | |||
| 3(a − b) | 3 |