styczne do wykresu funkcji f mr t: Ile z podanych niżej równań prostych są równaniami stycznych do wykresu funkcji f(x)=x³+x²−x y=1,

	5
y=−
	27

y=−x y=4x−3

mr t: początkowo robiłem przez podstawianie za y do równania f(x)=x³+x²−x poszczególnych równań i sprawdzałem, gdzie będę miał tylko jedno miejsce zerowe, jednak dla każdego z tych równań wychodziły mi dwa miejsca zerowe

Jerzy:

	5
y = 1 i y = −
	27

mr t:

	5
tzn. przykładowo prosta y=−		przecinała wykres funkcji f w dwóch miejscach, jak teraz
	27

sprawdzić, który z tych punktów jest właściwy?

mr t: @Jerzy wszystkie

Jerzy: Wskazówka: poszukaj ekstrema lokalne.

salamandra: Wydaje mi się, że powineneś sprawdzić czy dla punktów przecięcia prostej, z wykresem funkcji, jaka wychodzi styczna dla danego P i P'

mr t: @salamandra, możesz trochę rozwinąć? zwykle nie zrozumiałem o co chodzi

mr t:

	5
@Jerzy licząc po ekstremach wychodzi, że tylko proste y=1 i y=−		są styczne do wykresu.
	27

A wg. odpowiedzi wszystkie cztery proste są styczne do wykresu funkcji f

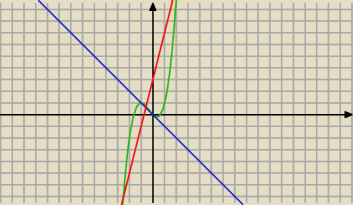
Jerzy: Tak, y = −x jest styczną,ale prosta: y = 4x + 3 z pewnoscią nie jest

Jerzy: Aj, tam jest y = 4x − 3

mr t: Jak to liczyłeś?

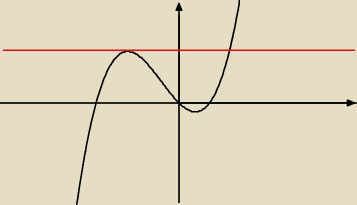
WhiskeyTaster: Styczne? Styczne. Przecina w dwóch miejscach? Przecina. Ogólnie styczna może przecinać wykres w więcej niż jednym punkcie. Spróbuj robić jak Jerzy radzi.

Sergiej: f(x) = x³ + x² − x f'(x) = 3x² + 2x − 1 Równanie stycznej w punkcie m y = f'(m)(x − m) + f(m) y = (3m² + 2m − 1)(x − m) + m³ + m² − m y = (3m² + 2m − 1)x − 2m³ − m²

	1
y = 3(m + 1)(m −		)x − m2(m + 1)
	3

i analizuj, które proste mogą być stycznymi

mr t: toż to dużo liczenia, to zadanie za 1pkt na maturze, nie miałbym tyle czasu

mr t: znalazłem ciut bardziej elegancki sposób, napiszę, może ktoś inny też skorzysta najpierw liczę pochodna funkcji f, następnie wiadomo, że a=f'(x) czyli:

	1
dla pierwszych dwóch równań: 3x2+2x−1=0, tutaj ewentualne punkty styczności to x=−1 x=		,
	3

	1
liczę f(−1) i f(		)
	3

dla trzeciego 3x²+2x−1=−1 i analogicznie dla czwartego 3x²+2x−1=4 i reszta analogicznie

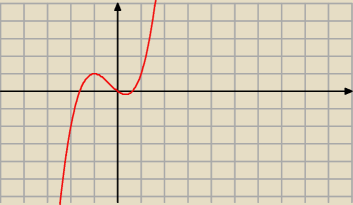
PW: Pochodna funkcji w punkcie x₀ to tamgens kąta nachylenia stycznej w punkcie (x₀, f(x₀)) do osi OX. Liczymy: f'(x) = 3x² + 2x − 1 Prosta y = 1 jest nachylona pod kątem 0°, a tg0° = 0. Sprawdzamy, czy istnieje x, dla którego f'(x) = 0 3x² + 2x − 1 = 0.

	1
Δ = 4 + 12 = 16 > 0, a więc istnieją dwa takie x: x0 = −1 i x1 =		(patrz wykres).
	3

Sprawdzamy, że dla x = − 1 jest f(x) = (−1)³+(−1)²−(−1) = 1. Prosta o równaniu y = 1 przechodząca przez punkt (−1, 1) jest styczną.. Istnieje jeszcze druga styczna równoległa do osi OX, ale nie jest to prosta, którą badamy (dla rozwiazania zadania nie jest istotna). Gybyśmy jednak ją wyznaczyli podstawiając

	1		1		1		1		5
f(		) = (		)3 + (		)2 −		= −		,
	3		3		3		3		27

	5
to stwierdzimy, że jest to styczna o równaniu y = −		(druga z podanych w treści
	27

zadania). \Podobnie z prostą y = − x. Tangens kąta nachylenia jest równy tg(135°) = − tg45° = − 1. Równość f'(x) = −1, tzn. 3x² + 2x − 1 = −1 3x² − 2x = 0

	2
ma miejsce dla x2 = 0 oraz dla x3 =		.
	3

Dla x₃ = 0 jest f(x₃) = 0 − styczna przechodzi przez punkt (0, 0) i ma równanie y = − x. Ewentualnej drugiej stycznej nachylonej pod kątem 135° już nie szukamy, nie jest potrzebna do rozwiązania zadania. Prosta y = 4x − 3 jest nachylona do osi OX pod takim kątem α, że tgα = 4. Równość; f'(x) = 4 czyli 3x² + 2x − 1 = 4 3x² − 2x − 5 = 0, Δ = 4 − 4•3•(−5) = 64

	5
ma miejsce dla x5 = −1 oraz dla x6 =		. Punktu x5 nie sprawdzamy, gdyż wykres ma już
	3

w punkcie (−1, f(−1)) styczną różną od y = 4x − 3. Dla x₆ mamy

	5		5		5		155
f(x6) = (		)3 + (		)2 −		=
	3		3		3		27

	5		20		11		155
4x6 − 3 = 4(		) − 3 =		− 3 =		≠		− prosta y = 4x − 3 nie jest
	3		3		3		27

styczna. Odpowiedź: Trzy spośród podanych prostych są styczne do wykresu funkcji.

PW: O licho, nie widziałem ostatniej wypowiedzi i niepotrzebnie się narobiłem

WhiskeyTaster: A tam niepotrzebnie, komuś kiedyś na pewno się przyda

ABC: ja bym to jeszcze skrócił uwagą że zbiór wartości pochodnej jest taki że wszystkie współczynniki kierunkowe tam należą a ty epopeję w trzynastu księgach rozpisałeś

PW: Nie rozumiem, co to ma do rzeczy, ale krytykę przyjmę z pokorą, gdy pokażesz jak to upraszcza rozumowanie.

Jerzy: ABC ma rację, to najprostsze uzasadnienie

PW: Przepraszam, ake uzasaadnieni czego? (patrz przypadek prostej y = 4x − 3).

Jerzy: Masz rację PW , to że prosta ma współczynnik naleleżący do zbioru warości pochodnej nie oznacza ,że musi być ona styczna do krzywej

PW: Tak

Jerzy: Dziwi mnie w takim razie,że jest to zadanie za 1 pkt.