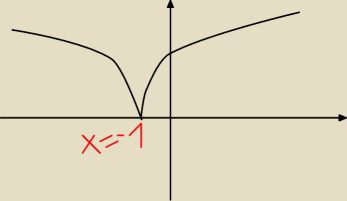
Problem z ekstremum i pochodną Ktostam: Mam funkcję f(x)=|x³+3x+4| i wygląda ona mniej więcej tak jak na rysunku. I mam pytanie odnośnie tego, czy jest możliwe, aby w punkcie x=−1 istniało ekstremum, co widać na załączonym obrazku, ale jednocześnie bez istnienia pochodnej w tym punkcie? No bo, kiedy obliczę pochodną z f(x) jako f(x)=√(x³+3x+4)², to wychodzi (2(x³+3x+4)(3x²+3))/2*√(x³+3x+4. No i ta pochodna istnieje dla x∊R za wyjątkiem miejsca, w którym zeruje się mianownik, czyli w x=−1, a wyraźnie widać, że znajduje się tam ekstremum minimum.

wredulus_pospolitus: To że pochodna w punkcie nie istnieje, to nie oznacza że nie może być w tym punkcie ekstremum Powyższa funkcja jest tego przykładem, innym dobrym przykładem jest g(x) = |x|