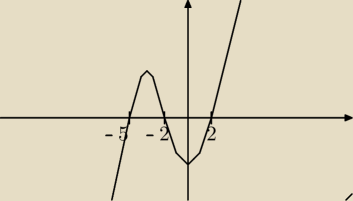
Na rysunku przedstawiony jest wykres funkcji W(x)=ax^2+bx+c Anon: Na rysunku przedstawiony jest wykres funkcji W(x)=ax²+bx+c A. a>0, b>0, c>0 B. a>0, b>0, c<0 C. a>0, b<0, c<0 D. a<0, b<0, c<0

ABC: kolego funkcja ax²+bx+c nie może mieć trzech miejsc zerowych

Leszek: To nie jest wykres funkcji W(x) ! ! ! Natomiast jest to wykres funkcji byc moze trzeciego stopnia ? ?

ABC: co autor zadania miał na myśli i za co kochamy autora?

Anon: wiem, że funkcja kwadratowa może mieć maksymalnie 2 miejsca zerowe, ale taki rysunek mam w poleceniu więc co poradzę

ABC: dawaj skan książki na zapodaj i linka tutaj

wredulus_pospolitus: to napisz nauczycielowi, aby puknął się w główkę i zastanowił się trochę zanim znowu da Ci takie zadanie do rozwiązania

a7:

	1
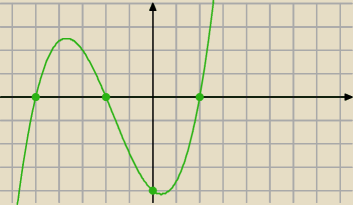
np. y=		(x+5)(x+2)(x−2)
	5

ICSP: no to panowie zakładamy, że W(x) = ax³ + bx + c która odpowiedź jest teraz poprawna?

Anon: chyba, że wzór funkcji to coś w stylu (x+5)(|x|−2)

Anon: fakt, prawidłowy wzór funkcji to W9X)=ax³+bx+c

Anon: *W(x)

Leszek: Poniewaz lim W(x) = ∞ , dla x→∞ to a >0 , zeby sprawdzic c to dla x=0 , W(0) <0 , c < 0 Dokoncz b .......

ABC: ale z tego rysunku wynika że funkcja jest postaci a(x−2)(x+5)(x+2) jakim cudem zniknie wyraz z x² ?

Anon: więc na pewno a>0, bo funkcja na końcu idzie do góry, c<0, bo dla x=0 funkcja przyjmuje wartość ujemną, ale b jak wpływa na wykres takiej funkcji?

a7: b<0

Anon: a skąd to wiadomo? pytam się, bo chciałbym wiedzieć na przyszłość, pierwszy raz robię tego typu zadanie

ABC: w każdym równaniu trzeciego stopnia gdzie znika współczynnik przy x² suma pierwiastków wynosi 0 a tu tak nie jest

Anon: Z tego co zrozumiałem te miejsca zerowe trzeba zignorować, liczy się wykres

a7: to znaczy normalnie to byłby prawidłowy przykład i byłoby np a>0, gdyż dla x→−∞ wykres byłby poniżej c<0, gdyż W(0)=c, a wykres przecina oś OY poniżej zera natomiast b liczymy albo metodą prób i błędów, albo, co jest chyba bardziej "profesjonalne" wynika to z pochodnej tj z faktu, że fukcja ma dwa ekstrema lokalne pochodna f'(x)=3x²+b teraz 3x²+b=0 x²=−b/3 x=±√^−b₃ to co pod ułamkiem musi być dodatnie, gdyż ekstrema istnieją czyli b musi być ujemne −b/3>0 czyli b<0

a7: PS> tutaj mamy "nieprawidłowy" przykład gdyż mamy jeszcze współczynnik np.d przy x², więc w ogóle zadanie jest chyba z błędem

a7: ale współczynnik przy x i tak jest ujemny natomiast d przy x² jest dodatni

Anon: Tak, brakuje dx², ale napisane miejsca zerowe wprowadzają w błąd i trzeba wziąć pod uwagę sam wykres. Więc nie wiem po co w ogóle zostały wypisane w zadaniu. W każdym razie dziękuję za wytłumaczenie

Anon: W części z pochodną funkcji powinno być równanie 3ax²+b=0, ale nadal wychodzi z tego, że −b>0, więc b<0

a7: tzn tutaj (w tym dziwnym przykładzie) w części z pochodna byłoby 3ax²+10dx+b istnieją dwa ekstrema więc Δ>0

	5d2
10d2−12ab>0 12ab<10d2 b<
	6a