Optymalizacja/pochodna
Jokur: Dana jest parabola y=8−x
2. Wyznacz największą wartość pola prostokąta ABCD zawartego pomiędzy
osią OX a parabolą, którego wierzchołki A i B leżą na osi OX, a wierzchołki C i D położone są
na paraboli.
Proszę o pomoc w rozwiązaniu. Mam problem z ułożeniem funkcji

12 maj 17:23
wredulus_pospolitus:
to pokaż co udało Ci się zrobić
12 maj 17:26
fil:
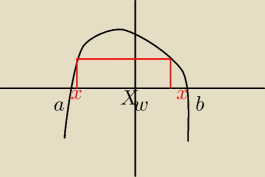
a, b − miejsca zerowe funkcji f
12 maj 17:28
Jokur: Udało mi się teraz ułożyć funkcję: f(x)=16x−2x3 Jest dobrze? (Pole mi wyszło y*2x)
12 maj 17:29
wredulus_pospolitus:
a czym jest 'x' u Ciebie

12 maj 17:30
ICSP: x > 0
P = 2x*(8 − x
2) = f(x)
| | 2√2 | |
f' = 16 − 6x2 = 0 ⇒ x0 = |
| |
| | 3 | |
Liczyłem w głowie, więc mogłem się pomylić.
12 maj 17:33
Jokur: y to współrzędna punktów wspólnych z parabolą, x to odległość punktu wspólnego z osią OX, więc
jeśli oś OY jest osią symetrii prostokąta to jego bok(podstawa) ma 2x
12 maj 17:33
Jokur: A jeszcze pytanie odnośnie dziedziny− wystarczy założyć, że x,y>0 ?
12 maj 17:34
adas4: Jak x >= √8 lub x <= −√8 to co sie wtedy dzieje?
12 maj 17:53
Jokur: wtedy warunki zadanie nie są spełnione, czyli x>−√8 i x<√8 oraz y<8
12 maj 17:58
Minato:
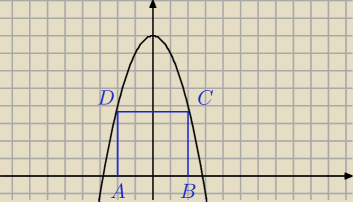
C=(x, 8−x
2), założenie x>0 i x <
√8 = 2
√2
|CD| = 2x
|BC| = 8−x
2
P(x) = 2x(8−x
2)=−2x
3+16x
P'(x) = −6x
2+16 = 0
P''(x) = −12x
| | 2√6 | | 2√6 | |
P''( |
| ) < 0 zatem w x = |
| mamy maksimum |
| | 3 | | 3 | |
12 maj 18:05
Jokur: Dziękuję bardzo wszystkim za pomoc

12 maj 18:14

 a, b − miejsca zerowe funkcji f
a, b − miejsca zerowe funkcji f

 C=(x, 8−x2), założenie x>0 i x < √8 = 2√2
|CD| = 2x
|BC| = 8−x2
P(x) = 2x(8−x2)=−2x3+16x
P'(x) = −6x2+16 = 0
C=(x, 8−x2), założenie x>0 i x < √8 = 2√2
|CD| = 2x
|BC| = 8−x2
P(x) = 2x(8−x2)=−2x3+16x
P'(x) = −6x2+16 = 0
