FUNKCJE
NIKINIKI:
1. Wyznacz równanie funkcji:
f(x)=3x2−2x+4 w punkcie (1;5)
2. Wyznacz ekstrema funkcji:
f(x)=2x3+3x2−12x−2
12 maj 15:43
ABC:
co rozumiesz przez "równanie funkcji" ?
12 maj 15:44
Jerzy:
Co to znaczy równanie funkcji w punkcie ?
12 maj 15:45
NIKINIKI: wyznacz równanie stycznej do wykresu funkcji (poprawiam 1 zad)
12 maj 15:49
Jerzy:
1) y = f'(1)*(x − 1) + f(1)
2) najpierw policz pochodną i znajdź jej miejsca zerowe
12 maj 15:51
NIKINIKI: pocogdna f'(x)=6x2+6x−12 nie ma mijesc zerowych
12 maj 16:01
Jerzy:
A dlaczego tak twierdzisz ?
12 maj 16:05
NIKINIKI: bo delta wychodzi −23
12 maj 16:05
ABC:
62−4*6*(−12) to jest −23?
12 maj 16:07
Jerzy:
6(x2 + x − 2) = 0 i Δ dla nawiasu = 1 + 8 = 9
12 maj 16:07
ABC:
normalnie też wychodzi ładnie 324 i pierwiastek 18
12 maj 16:09
Jerzy:
A bez Δ: x2 + 2x − x − 2 = (x + 2)(x − 1)
12 maj 16:12
NIKINIKI: i ekstrema funkcji wynosi 9 tak ?
12 maj 16:12
ABC:
jaki typ ...

12 maj 16:13
NIKINIKI: jeyne co mnie interesuje to ile ona wynosi

12 maj 16:14
ABC:
a jak jest więcej niż jedna ekstrema?
wiele lat temu jako młody chłopak sam byłem ekstremą solidarnościową

12 maj 16:17
Jerzy:
Jeśli masz dwa miejsca zerowe,to masz dwa ekstrema lokalne.
12 maj 16:19
NIKINIKI: ekstrema funkcji to min =(−2) a max = 1

12 maj 16:21
ABC:
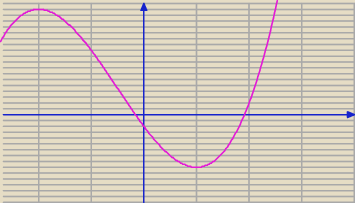
dokładnie odwrotnie patrz rysunek
12 maj 16:29


 a jak jest więcej niż jedna ekstrema?
wiele lat temu jako młody chłopak sam byłem ekstremą solidarnościową
a jak jest więcej niż jedna ekstrema?
wiele lat temu jako młody chłopak sam byłem ekstremą solidarnościową 
